Question 1203853: Suppose you are playing a game that involves rolling a 20-sided die. Before the game begins, you name a number called the threshold from 0 to 19. Then you roll the die until you exceed your threshold T. You have to pay $1 per roll and you get paid whatever is shown on the die at the end. What is the threshold that maximizes the expected profit?
example: T=7; roll 4, 2, 11. profit = $11- $3=$8.
Answer by ikleyn(52915)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Suppose you are playing a game that involves rolling a 20-sided die.
Before the game begins, you name a number called the threshold from 0 to 19.
Then you roll the die until you exceed your threshold T.
You have to pay $1 per roll and you get paid whatever is shown on the die at the end.
What is the threshold that maximizes the expected profit?
example: T=7; roll 4, 2, 11. profit = $11- $3=$8.
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
It is nice a Math circle or a Math Olympiad level problem.
Surely, the major part of the solution is to create an appropriate setup
(= to get an idea what to do and how to approach the solution).
Let T be the value of the threshold.
Then the probability to roll the number equal or lesser than threshold is 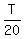 .
So, with the probability .
So, with the probability 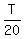 you will pay your first dollar, when your first rolled number will be <= T;
with the probability you will pay your first dollar, when your first rolled number will be <= T;
with the probability  you will pay your second dollar, when your second rolled number will be <= T;
with the probability you will pay your second dollar, when your second rolled number will be <= T;
with the probability 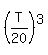 you will pay your third dollar, when your third rolled number will be <= T, and so on . . .
Thus the mathematical expectation of what you pay is the infinite sum of this geometric progression you will pay your third dollar, when your third rolled number will be <= T, and so on . . .
Thus the mathematical expectation of what you pay is the infinite sum of this geometric progression
 + + 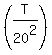 + + 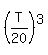 + . . . = + . . . = 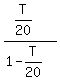 .
The mathematical expectation of what you will be payed back, when you finally
exceed the threshold, is the arithmetic mean between (T+1) and 20.
This arithmetic mean is .
The mathematical expectation of what you will be payed back, when you finally
exceed the threshold, is the arithmetic mean between (T+1) and 20.
This arithmetic mean is 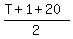 = = 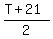 .
So, your final balance, expected after playing this game many times, is .
So, your final balance, expected after playing this game many times, is 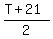 - - 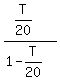 .
Now your task is to find the maximum of this function.
You can do it, using Calculus.
But I prefer to save my mind; so I prepared a table of values using Excel spreadsheet below
T .
Now your task is to find the maximum of this function.
You can do it, using Calculus.
But I prefer to save my mind; so I prepared a table of values using Excel spreadsheet below
T 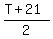 - - 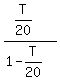 --------------------------------------------------
1 10.95
2 11.39
3 11.82
4 12.25
5 12.67
6 13.07
7 13.46
8 13.83
9 14.18
10 14.50
11 14.78
12 15.00
13 15.14
14 15.17 <<<---=== the maximum win (Math expectation)
15 15.00
16 14.50
17 13.33
18 10.50
19 1.00
The maximum value of the function is marked in the table.
The plot of the function is shown below.
--------------------------------------------------
1 10.95
2 11.39
3 11.82
4 12.25
5 12.67
6 13.07
7 13.46
8 13.83
9 14.18
10 14.50
11 14.78
12 15.00
13 15.14
14 15.17 <<<---=== the maximum win (Math expectation)
15 15.00
16 14.50
17 13.33
18 10.50
19 1.00
The maximum value of the function is marked in the table.
The plot of the function is shown below.
 Function y =
Function y = 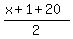 - - 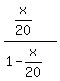 .
It should be read at 1 <= x <= 19.
ANSWER. The maximum win expectation is provided at the threshold value of T = 14 dollars. .
It should be read at 1 <= x <= 19.
ANSWER. The maximum win expectation is provided at the threshold value of T = 14 dollars.
Solved.
|
|
|