Question 1203815: Three machines turn out all the products in a factory, with the first machine producing 10% of the products, the second machine 15%, and the third machine 75%. The first machine produces defective products 6% of the time, the second machine 15% of the time and the third machine 8% of the time. What is the probability that a non-defective product came from the second machine? (Round your answer to four decimal places.
Answer by ikleyn(52777)   (Show Source):
You can put this solution on YOUR website! .
Three machines turn out all the products in a factory, with the first machine
producing 10% of the products, the second machine 15%, and the third machine 75%.
The first machine produces defective products 6% of the time, the second machine 15% of the time
and the third machine 8% of the time. What is the probability that a non-defective product
came from the second machine? (Round your answer to four decimal places.
~~~~~~~~~~~~~~~~~~~~~~~~
It is about calculating a conditional probability.
This conditional probability is the fraction, whose denominator is the probability
to get a non-defective product from all 3 machines, while the numerator
is the probability to get a non-defective product from second machine.
By knowing it, we write the formula immediately
P = 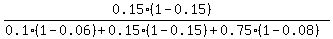 = 0.1399 (rounded as requested).
ANSWER. P = 0.1399 (rounded as requested).
Solved, with complete explanations.
|
|
|
