 That's the graph. Now we'll shade the area under it:
That's the graph. Now we'll shade the area under it:
 Now we find the area between the graph and the x-axis, take half
of it and find the value of x which divides the entire area into
two parts.
First we find the area under the curved (parabola) part
Now we find the area between the graph and the x-axis, take half
of it and find the value of x which divides the entire area into
two parts.
First we find the area under the curved (parabola) part
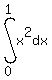



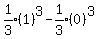

 The right part of the graph is just a rectangle with base 1 and height
The right part of the graph is just a rectangle with base 1 and height  ,
so its area is just
,
so its area is just  .
The entire shaded area is
.
The entire shaded area is 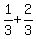

 So we need to find the value of x such that half the area
So we need to find the value of x such that half the area  is left of
it and the other half
is left of
it and the other half  , is on the right of it.
The area under the parabola is
, is on the right of it.
The area under the parabola is  so that leaves
so that leaves  the we must take
of the rectangle. To get the base of a rectangle with area
the we must take
of the rectangle. To get the base of a rectangle with area  that has height
that has height  ,
we divide the area by the height and get
,
we divide the area by the height and get 

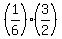

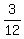

 . So the
median is
. So the
median is  on a unit past 1, or
on a unit past 1, or 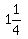 .
So the median is
.
So the median is 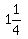 . To indicate the median, we can draw a green
vertical line through the graph at
. To indicate the median, we can draw a green
vertical line through the graph at  :
:
 Edwin
Edwin