Question 1203673: A softball team has three pitchers, A, B, and C, with winning percentages of 0,4, 0.6, and 0.8 respectively. These pitchers pitch with frequency 2,3 and 5 out of every 10 games, respectively In other words for a randomly selected game P(A) = 0.2 P(B) = 0.3, and P(C) = 0.5:
A) Find P(team wins game) = P(W)
B) P(A pitched game|team won) = P(A|W)
Found 2 solutions by ikleyn, math_tutor2020:
Answer by ikleyn(52790)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
A softball team has three pitchers, A, B, and C, with winning  rates of 0.4, 0.6, and 0.8 respectively. rates of 0.4, 0.6, and 0.8 respectively.
These pitchers pitch with frequency 2,3 and 5 out of every 10 games, respectively
In other words for a randomly selected game P(A) = 0.2 P(B) = 0.3, and P(C) = 0.5:
(a) Find P(team wins game) = P(W)
(b) P(A pitched game | team won) = P(A|W)
~~~~~~~~~~~~~~~~~~~~~
Part (a) solution
Pitcher A contributes to winning 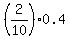 = 0.2*0.4 = 0.08.
Pitcher B contributes to winning = 0.2*0.4 = 0.08.
Pitcher B contributes to winning 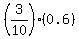 = 0.3*0.6 = 0.18.
Pitcher C contributes to winning = 0.3*0.6 = 0.18.
Pitcher C contributes to winning 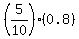 = 0.5*0.8 = 0.4.
The probability to win a game is the sum of these partial probabilities
P(W) = 0.08 + 0.18 + 0.4 = 0.66,
since their contributions are disjoint.
Part (b) solution
It is the conditional probability
P(A|W) = = 0.5*0.8 = 0.4.
The probability to win a game is the sum of these partial probabilities
P(W) = 0.08 + 0.18 + 0.4 = 0.66,
since their contributions are disjoint.
Part (b) solution
It is the conditional probability
P(A|W) = 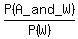 = = 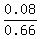 = 0.1212 (rounded). ANSWER = 0.1212 (rounded). ANSWER
Solved, with complete explanations.
=======================
I replaced the word "percentage" in the post, since there is NO any percentage there.
Simply the problem's creator likes to use "smart" scientific terms, but makes it lubberly.
Answer by math_tutor2020(3817)   (Show Source): (Show Source):
You can put this solution on YOUR website!
Part (a)
We have this information provided
P(A) = 0.2
P(B) = 0.3
P(C) = 0.5
and
P(W given A) = 0.4
P(W given B) = 0.6
P(W given C) = 0.8
Something like "P(W given A)" means "the probability of a win when we know 100% that pitcher A played".
P(W given A) = 0.4 can be rewritten to "P(W) = 0.4 when pitcher A plays"
This conditional probability formula
P(A given B) = P(A and B)/P(B)
rearranges to
P(A and B) = P(A given B)*P(B)
Then use the law of total probability
P(W) = P(W and A) + P(W and B) + P(W and C)
P(W) = P(W given A)*P(A) + P(W given B)*P(B) + P(W given C)*P(C)
P(W) = 0.4*0.2 + 0.6*0.3 + 0.8*0.5
P(W) = 0.66
-----------------------------------------
Part (b)
I'll use Bayes Theorem
P(A given B) = P(B given A)*P(A)/P(B)
So,
P(A given W) = P(W given A)*P(A)/P(W)
P(A given W) = 0.4*0.2/0.66
P(A given W) = 0.08/0.66
P(A given W) = 8/66
P(A given W) = 4/33
P(A given W) = 0.121212... where the "12" repeats forever
Round this however needed.
-----------------------------------------
Another approach for Part (a)
Let's say the team plays 100 games.
Pitcher A does 20% of those games, so they pitch for 0.2*100 = 20 games.
Pitcher B then does 0.3*100 = 30 games
Pitcher C then does 0.5*100 = 50 games
Here's the table so far
| Win | Loss | Total | | A pitches | | | 20 | | B pitches | | | 30 | | C pitches | | | 50 | | Total | | | 100 |
For the "A pitches" row, we'll have 8 wins and 12 losses.
This is because pitcher A has a 40% success rate, so they win 0.4*20 = 8 games and lose the other 20-8 = 12 games.
The other rows are filled out in a similar fashion.
We'll get this completed table
| Win | Loss | Total | | A pitches | 8 | 12 | 20 | | B pitches | 18 | 12 | 30 | | C pitches | 40 | 10 | 50 | | Total | 66 | 34 | 100 |
There are 66 wins out of 100 games total.
Therefore, P(W) = 66/100 = 0.66
-----------------------------------------
Another approach for Part (b)
Refer to the table in the previous section.
There are 66 wins. Of those wins, 8 are when pitcher A was in the game.
P(A given W) = P(A and W)/P(W)
P(A given W) = 8/66
P(A given W) = 4/33
P(A given W) = 0.121212...
We focus on the "win" column because we know 100% that a win occurred. We ignore the loss column.
|
|
|