Question 1203182: A medical researcher say that less than 25% of U.S. adults are smokers. In a random sample of 200 U.S. adults, 19.3% say that they are smokers. At alpha = 0.05, is there enough evidence to support the researcher's claim?
For the claim below, (a) identify the claim and state H0 and Ha, (b) find the critical value(s) and identify the rejection region(s), (c) find the standardized test statistic z, (d) decide whether to reject or fail to reject the null hypothesis, and (e) interpret the decision in the context of the original claim.
Answer by Theo(13342)   (Show Source): (Show Source):
You can put this solution on YOUR website! in a proportion typep study, p = the success rate for the test and q = the failure rate for the test.
the population mean is .25
the population p is thereforre .25 and the population q is .75 (their sum is always equal to 1).
the sample mean is .193
the sample p is therefore .193 and the sample q is .807
sample size is 200.
the standard error for the test is s = sqrt(.25 * .75 / 200) = .0306 when taken from the population mean.
the z-score formula is z = (x-m)/s
z is the z-score
x is the sample mean = sample p
m is the population mean = population p
s is the standard error for the test = population standard deviation divided by square root of sample size, as we derived above.
solve for z to get z = (.193 - .25) / .0306 = -1.867.
the area to the left of that z-score = .0312.
this means that the probability of getting a z-score less than -1.867 is approximately equal to 3%.
since the one tailed critical alpha on the low end is 5%, then the results of the test are significant, therefore supporting the claim that the real percentage is less than 25%.
i also used an online calculator to support these results.
here are the results from using that calculator.
first the inputs:
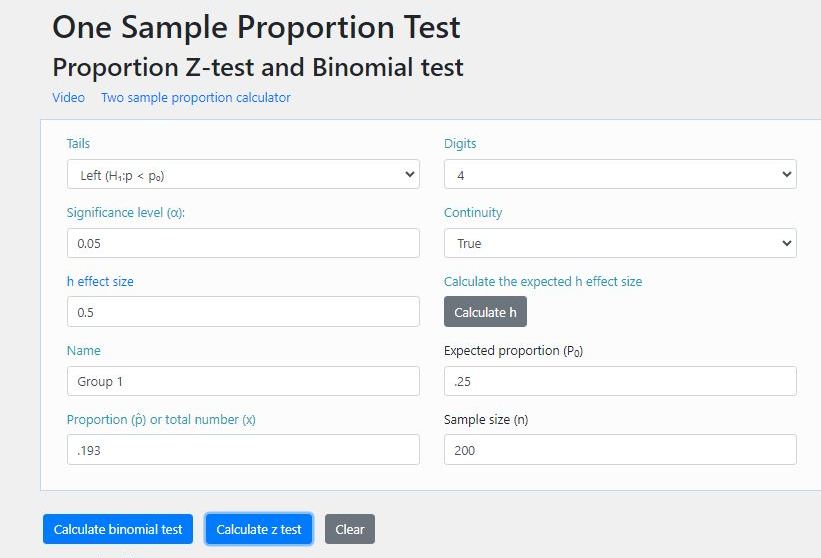
next the output:
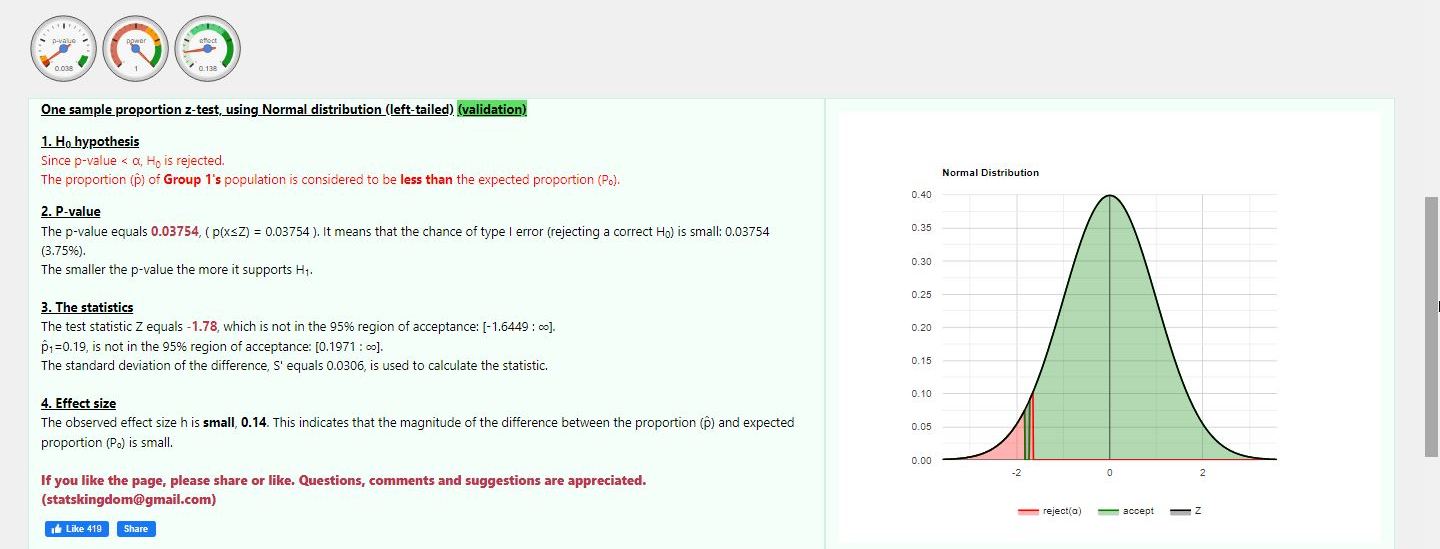
|
|
|