Question 1201897: What are the chances that a person who is murdered actually knew the murdered? The answer to this question explains why a lot of police detective work begins with relatives and friends of the victim. About 64% of people who are murdered actually knew the person who committed the murder. Suppose that a detective has 63 current unsolved murders.
What is the probability that at least 35 of the victims knew their murderers?
Found 2 solutions by Theo, ikleyn:
Answer by Theo(13342)   (Show Source):
You can put this solution on YOUR website! p = .64
q = .36
n = 63
assuming this is a binomial distribution type problem, i get the probability that at least 35 of the 63 victims knew their murderers is equal to 0.935075905.
the formula for the binomial distribution type of problem is p(x) = p^x * q^(n-x) * c(n,x).
since the number of calculations were large (x = 35 to 63), i used excel to do the arithmetic for me.
the sum of all the probbilities (x = 0 to 63) was equal to 1, as it should be.
Answer by ikleyn(52776)  (Show Source):
You can put this solution on YOUR website! .
What are the chances that a person who is murdered actually knew the murdered?
The answer to this question explains why a lot of police detective work begins
with relatives and friends of the victim. About 64% of people who are murdered
actually knew the person who committed the murder. Suppose that a detective has
63 current unsolved murders.
What is the probability that at least 35 of the victims knew their murderers?
~~~~~~~~~~~~~~~~~~~
The original problem is, of cource, a binomial distribution type.
But the number of trials is great: 63.
In such cases, the traditional approach is not to use the binopmial distribution formula.
The traditional approach is to use the normal distribution as an approximation
to the binomial distribution.
This normal distribution has the mean value n*p = 63*0.64 = 40.32 and the
standard deviation 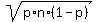 =  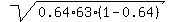= 3.80988 (rounded).
With it, our goal is to find the area under this normal curve on the right of the
raw mark 35; more precisely, taking the continuity correction factor, on the right
of the raw mark 34.5. You can use regular calculator TI-83 or TI-84
z1 z2 mean SD <<<---=== formatting pattern
P = normalcdf(34.5, 9999, 40.32, 3.80988).
You get the ANSWER 0.9367.
Solved.
------------------
So, doing this way, you can solve the problem using the traditional tools and methods
for an exam environment.
|
|
|
