Question 1201878: A BAG CONTAINS EIGHT CHIPS
NUMBERED 1 THROUGH 8. TWO CHIPS
ARE DRAWN RANDOMLY THE BAG AND
LAID DOWN IN THE ORDER THEY WERE
DRAWN. WHAT IS THE PROBABILITY
THAT THE 2-DIGIT NUMBER FORMED IS
DIVISIBLE BY 3?
Found 2 solutions by math_tutor2020, ikleyn:
Answer by math_tutor2020(3817)   (Show Source): (Show Source):
You can put this solution on YOUR website!
Answer: 5/14
5/14 = 0.357143 approximately
Explanation:
If the chip labeled "1" is selected 1st, then here are the other possible choices for the 2nd chip: 2,3,4,5,6,7,8
Once the chip is selected, we don't put it back.
Of those remaining choices only {2,5,8} will form a two digit number that starts with 1 and is a multiple of 3.
Those numbers being: 12, 15, 18
Notice the gap of 3 between adjacent terms.
Furthermore, notice the sum of the digits of any value gives 3 or a multiple of 3
1+2 = 3
1+5 = 6
1+8 = 9
If "2" was chosen first, then we could have any of these as the 2nd selection {1,4,7}. Again note the gap of 3 between terms.
21 --> 2+1 = 3
24 --> 2+4 = 6
27 --> 2+7 = 9
That shows we have multiples of 3.
This process is carried out for the remaining two digit numbers.
It might be faster to look at a multiplication table, or rely on your memorization of multiples of 3, to quickly get the values we want.
Keep in mind that- Repeat digits aren't allowed. Something like "33" won't work.
- We can't form numbers with the digit "0" in them (this chip label does not exist). This will rule out something like "30".
- We can't form numbers with the digit "9" in them (this chip label does not exist either). This rules out something like "39".
Here is the list of all two digit numbers that are multiples of 3, and that follow the criteria listed above
12, 15, 18, 21, 24, 27, 36, 42, 45, 48, 51, 54, 57, 63, 72, 75, 78, 81, 84, 87
There are 20 items in that list
This is out of 8*7 = 56 different two digit numbers possible that follow the criteria mentioned earlier.
20/56 = (4*5)/(4*14) = 5/14 is the final answer as a fraction.
5/14 = 0.357143 approximately
Answer by ikleyn(52781)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
In Excel, make a matrix of these two-digit numbers.
It is shown as Table 1 below.
T A B L E 1
----------------------------------------------------------
11 12 13 14 15 16 17 18
21 22 23 24 25 26 27 28
31 32 33 34 35 36 37 38
41 42 43 44 45 46 47 48
51 52 53 54 55 56 57 58
61 62 63 64 65 66 67 68
71 72 73 74 75 76 77 78
81 82 83 84 85 86 87 88
The matrix is 8x8 and contains 8*8 = 64 numbers in 64 cells.
Exclude its major diagonal from consideration.
So, actually the space of events has 64-8 = 56 elements.
Form another matrix placing in each cell the number mod(N,3), the sum of the digits modulo 3.
According to the divisibility by 3 rule, the sum of the digits modulo 3
is the same as mod(N,3).
This another matrix is shown below as Table 2.
T A B L E 2
----------------------------------------------------------
zeroes
- 0 1 2 0 1 2 0 3
0 - 2 0 1 2 0 1 3
1 2 - 1 2 0 1 2 1
2 0 1 - 0 1 2 0 3
0 1 2 0 - 2 0 1 3
1 2 0 1 2 - 1 2 1
2 0 1 2 0 1 - 0 3
0 1 2 0 1 2 0 - 3
In this Table, I placed "-" in the diagonal cells
(they do not participate in our consideration).
Calculate the number of cells with 0 (zero) contents.
The number of zeroes in each row is placed in the 9th column, for your convenience.
The number of zeroes in the Table 2 is 3+3+1 + 3+3+1 + 3+3 = 20.
Hence, the probability the problem is asking for is  = = 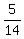 . ANSWER . ANSWER
Solved.
----------------
The divisibility by 3 rule, which I used in the solution, states that
Any positive integer number, divided by 3, gives the same remainder
as the sum of its digits divided by 3.
|
|
|