Question 1201861: The mean of a random variable X is E(X) = a, and the variance is D(X) = b. Find the probability P(X^2 < c).
(a = -0.09, b = 1.22, c = 1.77)
Answer by ikleyn(52781)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
The mean of a random variable X is E(X) = a, and the variance is D(X) = b.
Find the probability P(X^2 < c).
(a = -0.09, b = 1.22, c = 1.77)
~~~~~~~~~~~~~~~~~~~
The probability P(X^2 < c) is the same as the probability P( 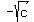 < X < < X <  ),
which is P = normalcdf( ),
which is P = normalcdf(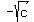 , ,  , a, , a, 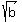 ), if you use a regular calculator
with standard function normalcdf, standing for normal cumulative distribution function.
Using given data, you can write
P = normalcdf( ), if you use a regular calculator
with standard function normalcdf, standing for normal cumulative distribution function.
Using given data, you can write
P = normalcdf(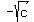 , ,  , a, , a, 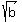 }) = normalcdf( }) = normalcdf(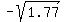 , , 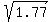 , -0.09, , -0.09, 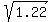 ) =
= normalcdf(-1.3304, 1.3304, -0.09, 1.1045) = 0.7701. ANSWER ) =
= normalcdf(-1.3304, 1.3304, -0.09, 1.1045) = 0.7701. ANSWER
Solved.
|
|
|