SOLUTION: Two people are selected at random from a group of eight women and ten men. Find the probability of the following. (See Example 9. Round your answers to three decimal places.) (a)

8 women + 10 men comprise 18 people, altogether.


Of 18 people, the number of different pairs of people is  
       =  = 9*17 = 153.


Of 8 women, the the number of different pairs of women is  
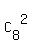       =  = 4*7 = 28.


Of 10 men, the the number of different pairs of men is  
       =  = 5*9 = 45.


So, the answer to question (a) is

    P =  =  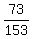= 0.477 (rounded).



To calculate the number of pairs, where at least one is woman, we subtract from 153
the number of pairs (man,man), which is 45

    153-45 = 108.



To answer question (b), we relate this number of 108 to 153

    P =  = 0.706 (rounded).