Question 1201704: WidgCo is a company that manufactures widgets. It is known that 1 out of every 50 widgets that the company produces is defective. A batch of 150 widgets is produced.
Find the probability that more than 5 widgets in the batch are defective.
Round your answer to 4 decimal places.
Answer by ikleyn(52943)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
WidgCo is a company that manufactures widgets. It is known that 1 out of every 50 widgets
that the company produces is defective. A batch of 150 widgets is produced.
Find the probability that more than 5 widgets in the batch are defective.
Round your answer to 4 decimal places.
~~~~~~~~~~~~~~~~~~~
It is a binomial distribution probability problem.
The number of trials is n= 150. The number of successful trials is "more than 5",
or k >= 6 (here the success is finding a defective widget). The probability of an individual success
is p = 1/50 = 0.02.
Since the number of trials is very big, the theory recommends to use a normal
approximation to binomial distribution.
The parameters of the normal approximation are
- the mean = 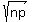 = = 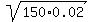 = =  = 1.732051 (rounded);
- the standard deviation SD = = 1.732051 (rounded);
- the standard deviation SD = 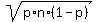 = = 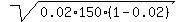 = 1.71464 (rounded).
So, we should find the area under the normal curve with the mean 1.732051 and standard deviation 1.71464282
on the right of the raw score 5.5 (using the continuity correction). Use the calculator normalcdf function
z1 z2 mean SD <<<---=== the formatting pattern
P = normcdf(5.5, 9999, 1.732051, 1.71464)
The answer is P = 0.014. = 1.71464 (rounded).
So, we should find the area under the normal curve with the mean 1.732051 and standard deviation 1.71464282
on the right of the raw score 5.5 (using the continuity correction). Use the calculator normalcdf function
z1 z2 mean SD <<<---=== the formatting pattern
P = normcdf(5.5, 9999, 1.732051, 1.71464)
The answer is P = 0.014.
Solved.
--------------------
Instead of using a regular calculator, you can use free of charge online calculator
https://onlinestatbook.com/2/calculators/normal_dist.html
////////////////////
A post-solution note
As a Math problem, it is not very well posed.
From one side, the number of trials is very big (150). Thus the "good style" does not leave us
the possibility to solve the problem as a binomial distribution and FORCES us to use
a normal distribution as an APPROXIMATION.
From the other side, formal requirements for applicability of the normal distribution approximation
(that are n*p >= 5) are not satisfied, so we can not expect that this approximation will be good.
It only allows to give an estimation of the order of a value, but does not allow to evaluate a value itself
with a perfect precision.
|
|
|