Question 1201610: Kevin has a bag with 8 balls numbered 1 through 8. He is playing a game of chance.
This game is this: Kevin chooses one ball from the bag at random. He wins $1 if the number 1 is selected, $2 if the number 2 is selected, $5 if the number 3 is selected, $6 if the number 4 is selected, $8 if the number 5 is selected, and $10 if the number 6 is selected. He loses $16 if 7 or 8 is selected.
(If necessary, consult a list of formulas.)
(a.) Find the expected value of playing the game.
(b.) What can Kevin expect in the long run, after playing the game many times?
(He replaces the ball in the bag each time.)
Answer by ikleyn(52778)   (Show Source):
You can put this solution on YOUR website! .
Kevin has a bag with 8 balls numbered 1 through 8. He is playing a game of chance.
This game is this: Kevin chooses one ball from the bag at random. He wins $1 if the number 1 is selected,
$2 if the number 2 is selected, $5 if the number 3 is selected, $6 if the number 4 is selected,
$8 if the number 5 is selected, and $10 if the number 6 is selected. He loses $16 if 7 or 8 is selected.
(If necessary, consult a list of formulas.)
(a) Find the expected value of playing the game.
(b) What can Kevin expect in the long run, after playing the game many times?
(He replaces the ball in the bag each time.)
~~~~~~~~~~~~~~~~~~
(a) The expected value of playing the game is
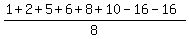 = 0 dollars.
If you need more explanations, learn the definition of an expected value from your textbook
or other source. It is the pre-requisite knowledge for this problem.
(b) In the long run, Kevin may expect that his average value (win or lose) will be close to zero.
Solved.
|
|
|
