Question 1201407: a) The prime Minister of a small Caribbean Island stated that 95% of the population was vaccinated from the Covid-19 virus. The opposition believes that the Minister is overstating the proportion of vaccinated citizens. He randomly selects 300 citizens and found that 240 of them were fully vaccinated. i. Calculate a 99% confidence interval for the true proportion of all citizens who were vaccinated. ii. Interpret you answer in i). iii. State the null and alternative hypothesis of this test. iv. Calculate the value of the test statistics. v. At the 5% level of significance, determine if the Politian overstated the proportion of vaccinated citizen. Use the classical approach.
Found 2 solutions by Theo, math_tutor2020:
Answer by Theo(13342)   (Show Source): (Show Source):
You can put this solution on YOUR website! claim is p = .95
sample size is 300
p from the sample is 240 / 300 = .8
95% confidence interval has z-score = plus or minus 1.96
z-score formula is z = (x-m)/s
z is the z-score
x is .8
m is .95
s is the standard error = sqrt(.95 * .05 / 300) = .0125830574
z-score formula becomes z = (.8-.95)/.0125830574 = -11.92.
this is well beyond the critical z-score of -1.96, indicating the results are significant.
the conclusion is that the roportiong is not .95, but more than likely something below that.
Answer by math_tutor2020(3817)   (Show Source): (Show Source):
You can put this solution on YOUR website!
Part (i)
p = population proportion of people who got vaccinated
n = sample size = 300
phat = sample proportion of people who got vaccinated = 240/300 = 0.80
At 99% confidence, the z critical value is roughly z = 2.576
Use a table like this
https://www.sjsu.edu/faculty/gerstman/StatPrimer/t-table.pdf
to get that value. Look at the bottom row labeled "Z" and above the 99% confidence level.
A stats calculator can also compute this value.
Compute the margin of error for the proportion.
E = z*sqrt(phat*(1-phat)/n)
E = 2.576*sqrt(0.80*(1-0.80)/300)
E = 0.0594901717373
E = 0.059490
This value is approximate.
Now we can compute the boundaries.
L = lower boundary of the confidence interval
L = phat - E
L = 0.80 - 0.059490
L = 0.74051
and
U = upper boundary of the confidence interval
U = phat + E
U = 0.80 + 0.059490
U = 0.85949
These values are approximate.
The 99% confidence interval in the format (L, U) is approximately (0.74051, 0.85949)
The 99% confidence interval in the format L < p < U is approximately 0.74051 < p < 0.85949
This second format is a bit more descriptive in terms of which population parameter we're trying to measure.
Side note:
An alternative confidence interval format is  which in this case is roughly which in this case is roughly 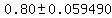
============================================================
Part (ii)
p = population proportion of people who got vaccinated
In the previous section we found 0.74051 < p < 0.85949
We are 99% confident the population proportion p is somewhere between 0.74051 and 0.85949
Meaning we are 99% confident the true percentage of people who got vaccinated is somewhere between 74.051% and 85.949%
Each percentage is approximate.
The percentage 95% is not in the interval between 74.051% and 85.949%, so it appears the opposition is correct in stating the true vaccination rate is below 95%.
============================================================
Part (iii)
p = population proportion of people who got vaccinated
Null: p = 0.95
Alternative: p < 0.95
The prime minister's claim is in the null hypothesis.
The opposition's claim is in the alternative hypothesis.
This is because the opposition believes the 95% vaccination rate is overstated (i.e. the value of p is lower).
This is a left-tailed test due to the "less than" sign in the alternative hypothesis.
If the test statistic is to the left of the critical value, then we reject the null.
============================================================
Part (iv)
p = 0.95 = hypothesized population proportion of people who got vaccinated
phat = sample proportion = 240/300 = 0.80
n = 300 = sample size
SE = standard error
SE = sqrt(p*(1-p)/n)
SE = sqrt(0.95*(1-0.95)/300)
SE = 0.01258305739211
This value is approximate.
Test statistic:
z = (phat - p)/SE
z = (0.80 - 0.95)/0.01258305739211
z = -11.9207912135929
z = -11.92
Test statistic: z = -11.92 approximately
============================================================
Part (v)
At the 5% level of significance, the left-tailed critical value is approximately z = -1.645 (use a table or stats calculator to determine this)
P(Z < -1.645) = 0.05 approximately
5% of the area under the standard normal Z curve is to the left of z = -1.645
We found that
test statistic = -11.92
critical value = -1.645
both of which are approximate
The test statistic is to the left of the critical value.
We're in the rejection region.
Therefore we reject the null and conclude p < 0.95 is the case.
Recall the confidence interval we found earlier was
0.74051 < p < 0.85949
meaning that the true vaccinated percentage is somewhere between 74.051% and 85.949% (we were 99% confident of this)
p = 0.95 is nowhere in the interval 0.74051 < p < 0.85949, so it is further evidence that the opposition may be onto something when stating the vaccination rate is below 95%
Conclusion: it appears the prime minister has likely overstated the vaccination rate. It's likely less than 95%.
|
|
|