Question 1200744: P% of the country's population have symptoms of a certain disease. When tested, a person with symptoms is diagnosed with a probability of p1, while a person without symptoms tests positive with a probability of p2. What is the probability that a randomly tested person will have a positive test result? What is the probability that a person who tested positive actually has symptoms of the disease? ([P, p1, p2] = [14, 0.96, 0.15])
Answer by ikleyn(52781)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
P% of the country's population have symptoms of a certain disease.
When tested, a person with symptoms is diagnosed with a probability of p1,
while a person without symptoms tests positive with a probability of p2.
(a) What is the probability that a randomly tested person will have a positive test result?
(b) What is the probability that a person who tested positive actually has symptoms of the disease?
([P, p1, p2] = [14, 0.96, 0.15])
~~~~~~~~~~~~~~~~~~~~~~
(a) The logic of the solution is as follows:
We have two disjoint sets: one "with the symptomps" and the other "without the symptoms".
If a person belongs to the first set, he contributes to the sough probability
with the weight p1;
if a person belongs to the second set, he contributes to the sough probability
with the weight p2.
It gives the ANSWER to question (a) 0.14*0.96 + (1-0.14)*0.15 = 0.2634.
(b) In the second question, they want you calculate a conditional probability.
So, this probability is the ratio of two values.
The denominator is the probability that a randomly chosen person is tested positively.
It is the probability which we just found out in part (a) above.
The numerator is the measure of the intersection of two sub-sets: those who has symptoms AND,
at the same time, are tested positively. So, the probability in the numerator is
0.14*0.96.
Thus the final expression and the value for this conditional probability is
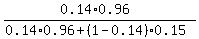 = 0.51025 (rounded). ANSWER = 0.51025 (rounded). ANSWER
Solved.
|
|
|