Question 1200691: 2. A certain casino claims that the commonly known phrase "The House Always Wins" does not apply to one of their games called “streak". In this game, players pay $2.00 for a chance to toss a coin until the outcome "tails" is observed for a maximum of four tosses (i.e., you can keep tossing until "tails” are observed). The casino pays the player $1.00 for each toss, so the longer your "streak” the better. Is the casino's argument right? (Hint: Argue for or against using the expected gain).
Found 2 solutions by greenestamps, ikleyn:
Answer by greenestamps(13216)   (Show Source): (Show Source):
You can put this solution on YOUR website!
The probability of getting tails on the first toss is 1/2; the payout is $1.
The probability of getting the first tails on the second toss (i.e., the outcomes are heads then tails) is (1/2)(1/2) = 1/4; the payout is $2.
The probability of getting the first tails on the third toss (i.e., the outcomes are heads, heads, and tails) is (1/2)(1/2)(1/2) = 1/8; the payout is $3.
The probability of getting the first tails on the fourth toss (i.e., the outcomes are heads, heads, heads, and tails) is (1/2)(1/2)(1/2)(1/2) = 1/16; the payout is $4.
So the expected payout to the player for the game is
(1/2)(1) + (1/4)(2) + (1/8)(3) + (1/16)(4) = 1/2 + 1/2 + 3/8 + 1/4 = 1 5/8
Since the game costs $2 to play, the house will win.
So the casino's claim that the house does NOT win in this game is false.
-----------------------------------------------------------------
The response from tutor @ikleyn uncovers an ambiguity in the statement of the problem.
Her (reasonable) interpretation is that if the player has a streak of 4 heads, then the house pays him $4 for the streak of 4.
My (also reasonable) interpretation is that, since the player never gets tails, the house pays him nothing.
Answer by ikleyn(52923)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
A certain casino claims that the commonly known phrase "The House Always Wins"
does not apply to one of their games called “streak".
In this game, players pay $2.00 for a chance to toss a coin until the outcome "tails"
is observed for a maximum of four tosses (i.e., you can keep tossing until "tails” are observed).
The casino pays the player $1.00 for each toss, so the longer your "streak” the better.
Is the casino's argument right? (Hint: Argue for or against using the expected gain).
~~~~~~~~~~~~~~~~~~~~~~
It is a typical " puzzle " style, when the formulation of an assignment is
unclear and incorrect at the same time.
I will explain it below, but first I want to give a small lecture about the casinos.
First, this statement "The House Always Wins" is factually INCORRECT, if to understand it literally.
Indeed, had it be so, the people would not visit casinos and would not play,
so that business would be dead. The feature is that people sometime win,
it is why they go to casinos. The casinos give them a chance, it is why they go
to casinos and why and how this business works.
The truth is that the casinos always win in average,
i.e. when the number of visitors, gamers and games is large.
But it is not applicable to every given concrete individual game.
Next issue is to discuss this problem's formulation itself and the solution, in particular.
The problem describes the game in this way (word-in-word)
players pay $2.00 for a chance to toss a coin until the outcome "tails" is observed
for a maximum of four tosses (i.e., you can keep tossing until "tails” are observed).
The casino pays the player $1.00 for each toss, so the longer your "streak” the better.
In this formulation, the criterion of stopping is defective.
Indeed, literally, the formulation says
"STOP when the TAIL is observed "AND" the number of tosses is <=4".
By the way, it is exactly a criterion used by @greenestamps in his solution.
But what to do if tail is NOT OBSERVED --and-- the number of tosses IS 4 ?
The criterion with the service word "AND" does not work in this case, so formally
the game must continue, while and although it is absurdist.
Thus, as given, the stopping criterion, obviously, is FATALLY ERRONEOUS:
it does not work properly. And, obviously, it is not that the authors meant.
The other, only possible criterion of stopping, is
"STOP when the TAIL is observed "OR" the number of tosses is 4".
It allows all possibilities listed in the solution by @greenestamp, PLUS one
additional possibility, missed in the solution by @greenestamp, namely,
the case when the number of tosses is 4 but TAIL is/was still not observed.
For clarity, the possible options are listed in the Table below
p o s i t i o n s Probability payment from the house
1 2 3 4 of this outcome obtained by the gamer
T 1/2 1
H T 1/4 2
H H T 1/8 3
H H H T 1/16 4
H H H H 1/16 4
It gives this Math expectation of winning
E = 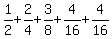 = = 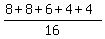 = =  .
Thus in this game, Math expectation to win is .
Thus in this game, Math expectation to win is  dollars.
But, paying 2 dollars for the participation, the gamer finally obtains dollars.
But, paying 2 dollars for the participation, the gamer finally obtains  = =  dollars, in average.
In other words, the gamer loses dollars, in average.
In other words, the gamer loses 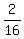 = =  of a dollar in each game, in average.
At the end, my answer is the same as that of @greenestamps, but my numbers are different. of a dollar in each game, in average.
At the end, my answer is the same as that of @greenestamps, but my numbers are different.
Resume of what is done:
- the stopping criterion is fixed,
and
- the accurate solution is obtained.
|
|
|