Question 1200590: A pair of symmetrical six-sided dice is rolled. If the sum equals k on the face up, player A wins and the game ends. If the sum is equal to m, B wins and there is no further betting. What is the probability that A wins after n rolls? What is the probability that B will win? ([n, k, m] = [17, 3, 6])
Answer by ikleyn(52932)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
A pair of symmetrical six-sided dice is rolled.
If the sum equals k on the face up, player A wins and the game ends.
If the sum is equal to m, B wins and there is no further betting.
(a) What is the probability that A wins after n rolls?
(b) What is the probability that B will win?
([n, k, m] = [17, 3, 6])
~~~~~~~~~~~~~~~~~~
(a) With the given data, the condition that A wins after n= 17 rolls is
that in previous 16 rolls the sum is NEITHER 3 NOR 6, but in the 17th roll the sum is 3.
The probability to get the sum 3 is  = =  .
The probability to get the sum 6 is .
The probability to get the sum 6 is 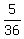 .
The probability do not have the sum 3 or 6 is .
The probability do not have the sum 3 or 6 is 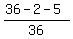 = = 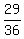 .
Thus the probability that A wins after 17 rolls is
P = .
Thus the probability that A wins after 17 rolls is
P = 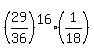 = 0.001747 (rounded). ANSWER = 0.001747 (rounded). ANSWER
Part (a) is complete.
Regarding part (b), the question (b) is unclear to me.
From the context, I can think that the question asks about the n=17th roll.
But I also may think that the question does not mean a concrete value of n.
My advise to you is NEVER put more than one question per post,
or, at least, to take care that your post and your questions are not ambiguous.
===============
On rolling dice problems see the lesson
- Rolling a pair of fair dice
in this site. You will find there many similar solved problems.
Read it and learn the subject from there. After that, you will be able easy solve such problems
ON YOUR OWN, which is your MAJOR GOAL visiting this forum (I believe).
|
|
|