Question 1200589: There are n stops on the bus route, the bus carries m passengers. Each of them gets off at one stop. What is the probability that no one gets off at at least one stop? What is the probability that no one gets off at exactly k stops? ([n, m, k] = [9, 13, 3])
Answer by ikleyn(52781)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
There are 9 stops on the bus route, the bus carries 13 passengers.
Each of them gets off at  one stop. one stop.
(a) What is the probability that no one gets off at at least one stop?
(b) What is the probability that no one gets off at exactly 3 stops?
~~~~~~~~~~~~~~~~~~
In this my post, I will solve part (b), ONLY.
I re-wrote the condition by substituting the given values
into the text directly, for easy reading and understanding.
We can select 3 stops from 9 stops in 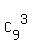 = =  = 84 ways.
So, for simplicity, we may think now that 3 stops are fixed, where no passengers go out.
At other 9-3 = 6 stops some passengers goes out (at least one).
So, the question now is:
+--------------------------------------------+
| In how many ways 13 passengers can be |
| separated/divided in 6 non-empty sets? |
+--------------------------------------------+
It is the same as to ask: how many solutions does this equation have = 84 ways.
So, for simplicity, we may think now that 3 stops are fixed, where no passengers go out.
At other 9-3 = 6 stops some passengers goes out (at least one).
So, the question now is:
+--------------------------------------------+
| In how many ways 13 passengers can be |
| separated/divided in 6 non-empty sets? |
+--------------------------------------------+
It is the same as to ask: how many solutions does this equation have
 + +  + +  + +  + + 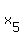 + + 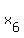 = 13 (*)
in integer positive numbers?
It is a typical problem to solve using the "stars and bars" method.
On Stars and Bars method, see this Wikipedia article
https://en.wikipedia.org/wiki/Stars_and_bars_(combinatorics)
or my lesson on the same subject in this site
Stars and bars method for Combinatorics problems
https://www.algebra.com/algebra/homework/Permutations/Stars-and-bars-method-for-Combinatorics-problems-2.lesson
The answer is: this equation (*) has = 13 (*)
in integer positive numbers?
It is a typical problem to solve using the "stars and bars" method.
On Stars and Bars method, see this Wikipedia article
https://en.wikipedia.org/wiki/Stars_and_bars_(combinatorics)
or my lesson on the same subject in this site
Stars and bars method for Combinatorics problems
https://www.algebra.com/algebra/homework/Permutations/Stars-and-bars-method-for-Combinatorics-problems-2.lesson
The answer is: this equation (*) has  = =  = 792 solutions.
THEREFORE, the answer to question (b) is P = = 792 solutions.
THEREFORE, the answer to question (b) is P = 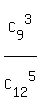 = = 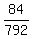 = = 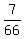 = 0.106061.
ANSWER to question (b) is P = = 0.106061.
ANSWER to question (b) is P = 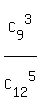 = = 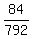 = = 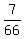 = 0.106061. = 0.106061.
Solved.
|
|
|