Question 1200086: Five fair coins were tossed simultaneously. What is the probability of getting three heads and two tails?
A. 1/32
B. 1/16
C. 1/8
D. 1/4
Found 3 solutions by math_tutor2020, greenestamps, ikleyn:
Answer by math_tutor2020(3817)   (Show Source): (Show Source):
You can put this solution on YOUR website!
Answer: A. 1/32
Reason:
I'm assuming the instructions "What is the probability of getting three heads and two tails?" refer to the exact order of 3 heads in a row, followed by 2 tails in a row.
Each side has probability 1/2
The probability of 3 heads in a row is (1/2)^3 = 1/8
The probability of 2 tails in a row is (1/2)^2 = 1/4
Multiply those results: (1/8)*(1/4) = 1/32
Or you could do a shortcut to say (1/2)^5 = 1/32
Answer by greenestamps(13200)   (Show Source): (Show Source):
You can put this solution on YOUR website!
The wording of the problem most definitely does NOT say the 5 outcomes are 3 heads followed by 2 tails in that order....
The number of possible outcomes on 5 flips of the coin is 2^5 = 32.
The number of ways (different orders) of getting 3 heads and 2 tails is the number of different ways of arranging the letters HHHTT. By a well-known counting principle, that number of ways is  . .
So the probability of getting 3 heads and 2 tails is 10/32 = 5/16.
Note for problems involving flipping fair coins, a familiarity with Pascal's Triangle is helpful. The 5th row of Pascal's Triangle is
1 5 10 10 5 1
Those numbers represent, respectively, the numbers of different ways of getting 5, 4, 3, 2, 1, or 0 heads.
Answer by ikleyn(52788)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
In this problem, the formulation is NOT CONSISTENT with the answers list.
As the post is worded, printed, and presented, its context means that the order of the three heads and two tails
is arbitrary. We can not make other assumptions.
If the order is special, it MUST be pointed in the problem explicitly.
Without special pointing, the meaning of the post is UNIQUE, by default: the order is  . .
If so, then this problem is a typical binomial distribution
with the number of trials n=5; the number of success k=3 (head);
and the probability of the individual success p =  .
Then the probability under the problem question is
P = P(n=5; k=3; p=0.5) = .
Then the probability under the problem question is
P = P(n=5; k=3; p=0.5) = 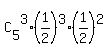 = = 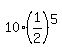 = = 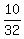 . ANSWER (which is not in the answers list). . ANSWER (which is not in the answers list).
Again: as written, the problem admits only one interpretation, regarding the order: the order is ARBITRARY.
If you want interpret in different way, then the wording must be changed adequately .
---------------
It is a standard rule in Math, interpreting texts by default:
By default, we assume the weakest assumption (which in this case is arbitrary ordering).
Everything which is more special than weakest, must be specified explicitly.
|
|
|