Question 1200014: A simple gambling game involves the throw of a die. Players are charged 40 cents if the die shows 1,2 or 3 they are charged nothing for 4 and they receive 30 cents or 60 cents respectively for 5 or 6. Let the random variable X be the payout to the player.
Calculate the expected value and how much profit would the casino expect to make on 100 games?
If the backer weighted the die so that it is 50% more likely to turn up each of the results 1,2,3 as to turn up 4,5 or 6.
What is the probability now of each outcome?
Find expected value now.
Found 2 solutions by math_tutor2020, ikleyn:
Answer by math_tutor2020(3817)   (Show Source): (Show Source):
You can put this solution on YOUR website!
Problem 1: A simple gambling game involves the throw of a die.
Players are charged 40 cents if the die shows 1,2 or 3 they are charged nothing for 4 and they receive 30 cents or 60 cents respectively for 5 or 6.
Let the random variable X be the payout to the player.
Calculate the expected value and how much profit would the casino expect to make on 100 games?
X = payout, in cents, to the player
X can take on the following values: {-40,0,30,60}
The negative value is where the player loses money.
The probability of rolling a 1, 2 or 3 is 3/6.
This is the probability of X = -40 happening.
The probability of rolling a 4 is 1/6 because there's one side labeled "4" out of 6 sides total.
This is when X = 0
The probability of rolling a 5 is also 1/6.
This is the probability of X = 30 happening.
The probability of rolling a 6 is also 1/6.
This is the probability of X = 60 happening.
Let's set up a table with each X and P(X) value.
| X | P(X) |
| -40 | 3/6 |
| 0 | 1/6 |
| 30 | 1/6 |
| 60 | 1/6 |
Now multiply across the rows to form the X*P(X) column.
Example: -40 times 3/6 = -120/6
| X | P(X) | X*P(X) |
| -40 | 3/6 | -120/6 |
| 0 | 1/6 | 0/6 |
| 30 | 1/6 | 30/6 |
| 60 | 1/6 | 60/6 |
Add the items in that third column to get the expected payout.
(-120/6)+(0/6)+(30/6)+(60/6)
= (-120+0+30+60)/6
= -30/6
= -5
A negative payout means the player lost money.
The player expects to lose, on average, 5 cents per game.
From the perspective of the casino, they are winning 5 cents per game on average.
Over the course of 100 games, the casino would expect to gain 100*5 = 500 cents = $5
Or the calculation would be 100*(0.05 dollars) = 5 dollars.
Answers:
Expected payout per game = -5 cents (perspective of the player)
Casino profit on one hundred games = $5
========================================================
Problem 2: If the backer weighted the die so that it is 50% more likely to turn up each of the results 1,2,3 as to turn up 4,5 or 6.
What is the probability now of each outcome?
Find expected value now.
50% more likely involves the multiplier 1.5, which converts to 3/2.
Rolling a 1,2, or 3 initially had probability 3/6 aka 1/2.
Increase that by 50% to get (1.5)*(1/2) = (3/2)*(1/2) = 3/4
Therefore, event X = -40 has probability P(X) = 3/4
On this weighted die, rolling a 1,2, or 3 has probability 3/4.
That means 1-3/4 = 1/4 is the leftover amount for the other values
Split that remaining bit into three equal pieces: (1/4)*(1/3) = 1/12
Rolling a 4 has probability 1/12
Rolling a 5 has probability 1/12
Rolling a 6 has probability 1/12
The event X = 0 has probability 1/12
The event X = 30 has probability 1/12
The event X = 60 has probability 1/12
| X | P(X) |
| -40 | 3/4 |
| 0 | 1/12 |
| 30 | 1/12 |
| 60 | 1/12 |
For the sake of consistency, let's get each denominator to 12.
3/4 = (3/4)*(3/3) = 9/12
| X | P(X) |
| -40 | 9/12 |
| 0 | 1/12 |
| 30 | 1/12 |
| 60 | 1/12 |
Now form the X*P(X) column
| X | P(X) | X*P(X) |
| -40 | 9/12 | -360/12 |
| 0 | 1/12 | 0/12 |
| 30 | 1/12 | 30/12 |
| 60 | 1/12 | 60/12 |
Add the X*P(X) items
(-360/12)+(0/12)+(30/12)+(60/12)
= (-360+0+30+60)/12
= -270/12
= -22.50
The player expects to lose, on average, 22.50 cents per game.
The casino expects to gain, on average, 22.50 cents per game.
Playing 100 games means the casino expects to make 0.225*100 = 22.50 dollars
Answers:
The probability of each outcome is shown in the table above
Expected payout for the player = -22.5 cents
Answer by ikleyn(52782)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
A simple gambling game involves the throw of a die.
Players are charged 40 cents if the die shows 1,2 or 3 they are charged nothing
for 4 and they receive 30 cents or 60 cents respectively for 5 or 6.
Let the random variable X be the payout to the player.
Calculate the expected value and how much profit would the casino expect to make on 100 games?
If the backer weighted the die so that it is 50% more likely to turn up
each of the results 1,2,3 as to turn up 4,5 or 6.
What is the probability now of each outcome?
Find expected value now.
~~~~~~~~~~~~~~~~~~~~~~
I agree with the solution of the first problem given by @math_tutor2020.
But regarding the second problem in the post, I read and interpret it differently;
therefore, my solution, my numbers and my answer are different.
In the second problem, we have six events 1, 2, 3, 4, 5 and 6, and we are given that
P(1) = P(2) = P(3); P(4) = P(5) = P(6)
and
P(1) = 1.5*P(4); P(2) = 1.5*P(5); P(3) = 1.5*P(6).
Let x be any of the three equal values P(4) = P(5) = P(6).
Then any of the three other equal values P(1) = P(2) = P(3) is 1.5x (it is where and how the multiplier 1.5 works in my solution).
The sum of probabilities P(1) + . . . + P(6) is 1. It gives this equation
3*(1.5x) + 3x = 1, or 4.5x + 3x = 1, or 7.5x = 1,
which implies
x =  = =  ; 1.5x = ; 1.5x = 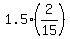 = =  .
Thus P(1) = P(2) = P(3) = .
Thus P(1) = P(2) = P(3) =  ; P(4) = P(5) = P(6) = ; P(4) = P(5) = P(6) =  .
Now math expectation of the player/(the gamer) is .
Now math expectation of the player/(the gamer) is
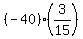 + + 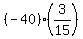 + + 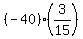 + + 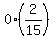 + + 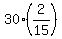 + + 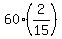 =
= =
=  = = 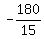 cents = -12 cents.
Which means that the gamer loses 12 cents per game, in average.
ANSWER. Math expectation is -12 cents: the gamer loses 12 cents per game, in average. cents = -12 cents.
Which means that the gamer loses 12 cents per game, in average.
ANSWER. Math expectation is -12 cents: the gamer loses 12 cents per game, in average.
Solved.
|
|
|