SOLUTION: A coin is Twice as likely to turn up Head as Tails in a sequences of independent tosses of the coin. What is the probability that the 3rd Head occurs on the 6th tosses.

From the problem,  P(Head) = 2/3;  P(Tail) = 1/3.


Next, the event that the 3rd Head occurs on the 6th toss is the intersection of two independent events, A and B.


    Event A is that in the first 5 tosses the Head will occur exactly two times.

    Event B is that the 6th toss will be Head.


Event A is the binomial with the number of trials n= 5, number of success trials k= 2
and the probability of success (=Head) of 2/3;  so

    P(A) = 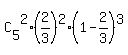 =  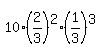= 0.164609.


For event B,  P(B) = P(Head) = 2/3.


Therefore,  P(A and B) = P(A)*P(B) = 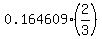 = 0.109739  (rounded).    ANSWER