.
A large company has an inspection system for the batches of new clutches purchased
from vendors. A batch typically contains 37 clutches. In the inspection system
a random sample of 19 
is selected and all are tested.
Suppose that there are 11 faulty clutches in the batch of 37 .
What is the probability that for a given sample there will be 
6 faulty clutches?
~~~~~~~~~~~~~~~~~~~~~
I edited your post to make its meaning absolutely clear and unambigous.
The probability in this problem is a ratio, whose denominator is the number of combinations
of 37 clutches taken 19 at a time
= 17672631900.
To calculate this great number, I used standard Excel function COMBIN(N,n).
It makes calculations faster than I can blink my eyes.
The numerator is the number of all possible 19-tuples of clutches, containing 6 of 11 faulty clutches.
These special 19-tuples are of the form (6 of 11 faulty clutches, 19-6=13 of 37-11=26 good clutches), and their number is
= 
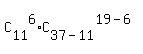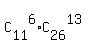= 462*10400600 = 4805077200.
Again, the number of combinations in this formula I calculated using Excel function COMBIN.
Thus the final probability is P =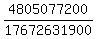 
= 0.2719 (rounded). ANSWER
Solved.
