Question 1197941: In the following problem, check that it is appropriate to use the normal approximation to the binomial. Then use the normal distribution to estimate the requested probabilities.
It is estimated that 3.5% of the general population will live past their 90th birthday. In a graduating class of 781 high school seniors, find the following probabilities. (Round your answers to four decimal places.)
(a) 15 or more will live beyond their 90th birthday
(b) 30 or more will live beyond their 90th birthday
(c) between 25 and 35 will live beyond their 90th birthday
(d) more than 40 will live beyond their 90th birthday
Answer by ewatrrr(24785)   (Show Source): (Show Source):
You can put this solution on YOUR website! Binomial Distribution:
n = 781 , p = .035
781*.035 and 781*.965 are > 5
Using the normal approximation and continuity correction factor.
(the continuity correction factor used as a Binomial Distribution is not continuous)
mean =781*.035= 27.335
sd = 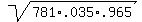 = 5.136 = 5.136
Using TI or similarly an inexpensive calculator like an Casio fx-115 ES plus
P(x ≥ 15 ) = normpdf(-9999 14.5, 27.335,5.136)= .0062
P(x ≥ 30 ) = normpdf(-9999 29.5, 27.335,5.136)= .6633
P( 25 ≤ x ≤ 35) = normcdf( 24.5,35.5, 27.335,5.136) = .6536
P(x > 40) = normpdf(40.5,9999, 27.335,5.136) = .0052
|
|
|