Question 1197870: 71% of all voters favor Proposition A and a random sample of 200 voters is taken. Use the normal approximation to the bonomial to find the following probabilities rounded to 3 decimal places.
a. Find the probability that more than 140 of the voters favor Proposition A. Incorrect
b. Find the probability that at most 150 of the voters favor Proposition A. Incorrect
c. Find the probability that between 141 and 149, inclusive, of the voters favor Proposition A.
Found 2 solutions by ewatrrr, ikleyn:
Answer by ewatrrr(24785)   (Show Source): (Show Source):
You can put this solution on YOUR website! Binomial Distribution:
n = 200, p = .71
Using the normal approximation and the NOted continuity correction factor.
(the continuity correction factor used as a Binomial Distribution is not continuous)
Using the normal approximation:
mean = 200*.71 = 142
sd = 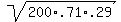 = 6.42 = 6.42
Using hand-held TI or similarly an inexpensive calculator like an Casio fx-115 ES plus
P(x > 140 ) = normpdf(140.5,9999 142, 6.42)= .592
P(x ≤ 150) = normcdf(-9999, 150.5,142, 6.42)= .907
P( 141 ≤ x ≤ 149) = = normcdf( 140.5,149.5, 142, 6.42) = .471
Answer by ikleyn(52943)   (Show Source): (Show Source):
You can put this solution on YOUR website! Probability-and-statistics/1197870:
.
71% of all voters favor Proposition A and a random sample of 200 voters is taken.
Use the normal approximation to the bonomial to find the following probabilities rounded to 3 decimal places.
a. Find the probability that more than 140 of the voters favor Proposition A. Incorrect
b. Find the probability that at most 150 of the voters favor Proposition A. Incorrect
c. Find the probability that between 141 and 149, inclusive, of the voters favor Proposition A.
~~~~~~~~~~~~~~~~~~~~~~
You have a binomial distribution with large number of trials n = 200
and individual probability of success p = 0.71.
You want to approximate it by the normal distribution.
You should use the mean value m = p*n = 0.71*200 = 142 and standard deviation
SD = 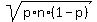 = = 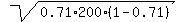 = 6.417.
Also, you should use the continuity correction factor.
About approximation of the binomial distribution by normal distribution and continuity correction factor
see your textbook and/or these Internet sources
https://www.statisticshowto.com/probability-and-statistics/binomial-theorem/normal-approximation-to-the-binomial/
https://online.stat.psu.edu/stat414/lesson/28/28.1
https://stats.libretexts.org/Courses/Las_Positas_College/Math_40%3A_Statistics_and_Probability/06%3A_Continuous_Random_Variables_and_the_Normal_Distribution/6.04%3A_Normal_Approximation_to_the_Binomial_Distribution
For calculations, you may use your calculator (function normcdf), or Excel spreadsheet (function NORMDIST);
or online calculator https://onlinestatbook.com/2/calculators/normal_dist.html
(a) In this case, you should find the area under the normal curve on the right from 140.5
(using the correction factor)
P(x > 140) = normcdf(140.5, 9999, 142, 6.417) = 0.592 (rounded).
(b) In this case, you should find the area under the normal curve on the left from 150.5
(using the correction factor)
P(x <= 150) = normcdf(-9999, 150.5, 142, 6.417) = 0.907 (rounded).
(c) In this case, you should calculate the area under the normal curve between 140.5 and 149.5
(using the correction factor)
P(141 <= x <= 149) = normcdf(140.5, 149.5, 142, 6.417) = 0.471 (rounded). = 6.417.
Also, you should use the continuity correction factor.
About approximation of the binomial distribution by normal distribution and continuity correction factor
see your textbook and/or these Internet sources
https://www.statisticshowto.com/probability-and-statistics/binomial-theorem/normal-approximation-to-the-binomial/
https://online.stat.psu.edu/stat414/lesson/28/28.1
https://stats.libretexts.org/Courses/Las_Positas_College/Math_40%3A_Statistics_and_Probability/06%3A_Continuous_Random_Variables_and_the_Normal_Distribution/6.04%3A_Normal_Approximation_to_the_Binomial_Distribution
For calculations, you may use your calculator (function normcdf), or Excel spreadsheet (function NORMDIST);
or online calculator https://onlinestatbook.com/2/calculators/normal_dist.html
(a) In this case, you should find the area under the normal curve on the right from 140.5
(using the correction factor)
P(x > 140) = normcdf(140.5, 9999, 142, 6.417) = 0.592 (rounded).
(b) In this case, you should find the area under the normal curve on the left from 150.5
(using the correction factor)
P(x <= 150) = normcdf(-9999, 150.5, 142, 6.417) = 0.907 (rounded).
(c) In this case, you should calculate the area under the normal curve between 140.5 and 149.5
(using the correction factor)
P(141 <= x <= 149) = normcdf(140.5, 149.5, 142, 6.417) = 0.471 (rounded).
Solved.
---------------
If you are a beginner student in learning probability distributions, I advise you to start learning
this kind of computations using the online calculator, to which I referred above.
It provides a graphical support, so at each step you do understand what you are doing.
In addition, this graphical support prevents you from making mistakes.
When you learn enough this kind of computations, you can switch to your regular calculator,
but even then you may use the online calculator for checking purposes.
|
|
|