Question 1197385: An ant moves on the following lattice, beginning at the dot labeled $A$. Each minute he moves to one of the dots neighboring the dot he was at, choosing from among its neighbors at random. What is the probability that after $5$ minutes he is at the dot labeled $B$? Image is attached below.
Found 3 solutions by lotusjayden, ikleyn, greenestamps:
Answer by lotusjayden(18)   (Show Source): (Show Source):
You can put this solution on YOUR website! Image is here: https://latex.artofproblemsolving.com/d/0/4/d04c14a38efb837151549f4b864fde841fa50f95.png
 . .
----------------------------------------------------------------------------
Answer(since I originally answered the question in Latex, and since It's almost time to sleep, I will edit it tomorrow.)(The original post is here: https://artofproblemsolving.com/texer/yglroond)
Color the dots red and blue shown below.. Notice that whenever the ant moves, it moves from a red dot to a blue dot or a blue dot to a red dot. So since  is a red dot, it must move to a blue dot, then a red dot, then a blue dot, then a red dot, and end up on a blue dot. There are only four blue dots, and the ant is equally likely to end up on any one of these four, since the diagram is symmetric to a is a red dot, it must move to a blue dot, then a red dot, then a blue dot, then a red dot, and end up on a blue dot. There are only four blue dots, and the ant is equally likely to end up on any one of these four, since the diagram is symmetric to a  rotation. The probability that the ant ends on rotation. The probability that the ant ends on  after five minutes is therefore after five minutes is therefore  . .
 . .
Note: @Ikleyn is not correct unlike the other times I saw her answer questions. The correct ones are me and @greenstamps.
Answer by ikleyn(52776)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Let E denotes one step horizontally in (+) direction (East)
W denotes one step horizontally in (-) direction (West)
N denotes one step vertically in (+) direction (North)
S denotes one step vertically in (-) direction (South).
We will denote each path as a sequence of letters E, W, N, S.
To get from A to B in 5 steps, the path must contain 5 letters; equal number of E and W letters;
in addition, the number of N letters must be 1 more than the number of S letters.
So, all good paths must fall into one of these DISJOINT categories
(1) no E,W at all; there are only all distinguishable permutations of 3N and 2S.
the number of such arrangements is 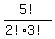 = =  = 10.
(2) one E compensated by one W, in any order; the rest are 2N and 1S in any arrangement.
the total number of such arrangements is = 10.
(2) one E compensated by one W, in any order; the rest are 2N and 1S in any arrangement.
the total number of such arrangements is 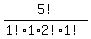 = =  = 60.
(3) two E compensated by two W, in any order; and only one N; no S
the total number of such artranjements is = 60.
(3) two E compensated by two W, in any order; and only one N; no S
the total number of such artranjements is 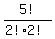 = = 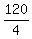 = 30.
Thus, there are 10 + 60 + 30 = 100 good arrangements (paths leading from A to B).
The total number of all possible paths of the length 5 is = 30.
Thus, there are 10 + 60 + 30 = 100 good arrangements (paths leading from A to B).
The total number of all possible paths of the length 5 is 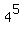 = 1024: any of 4 letters in each of 5 positions, independently.
So the probability is P = = 1024: any of 4 letters in each of 5 positions, independently.
So the probability is P = 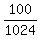 = = 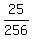 = 0.09766 (rounded). ANSWER = 0.09766 (rounded). ANSWER
Solved.
--------------
Nice contest/entertainment problem of a Math Olympiad or Math Circle level.
As a pre-requisite, you must know everything about distinguishable permutations.
About it, read the lesson
- Arranging elements of sets containing indistinguishable elements
in this site.
/////////////
In this post, the diagram attached by the visitor at the end,
DOES NOT correspond to the wording part of the problem - it creates misunderstanding.
In this problem, much wider lattice should be considered - otherwise, the probabilities
would not be all equal to 1/4 for moving one step from each current point.
Answer by greenestamps(13198)   (Show Source): (Show Source):
You can put this solution on YOUR website!
The analysis by tutor @ikleyn to find the number of ways to end at B is good. But her answer to the question is flawed, because there are not always 4 choices of a direction to go from a given vertex; the total number of possible paths of length 5 starting from point A on the lattice is far less than 4^5.
In the end, I believe the problem has a very simple solution and answer.
In 5 moves on the given lattice, the only points where the ant can end up are the four points 1 unit away from A. Point B is one of those four points; and the symmetry of the lattice means there is equal probability of ending up at any one of those four points.
So the probability of ending at B after 5 moves is 1/4.
ANSWER: 1/4
---------------------------------------------------------------
Response to tutor @ikleyn....
What an absurd note from you regarding my response to the question!
Did you take any time to read my response? or were you just reacting to the idea that anyone would dare to disagree with you?
I will not agree with you when you are WRONG!
The path EEEEE, starting from point A on the lattice, is not possible -- it goes off the lattice. In fact, it is obvious (to anyone who is paying attention to the problem) that a path EEEEE is not possible from ANY point on the lattice.
In your effort to show your superiority (?) in all things mathematical, you might try paying attention to the problem that you are working on.
|
|
|