Question 1197245: A game involving tossing 2 coins and receiving 58 cents if they are both heads what is a fair price to pay for the privilege of playing this game twice
Found 3 solutions by MathLover1, math_tutor2020, ikleyn:
Answer by MathLover1(20849)   (Show Source):
Answer by math_tutor2020(3817)  (Show Source):
You can put this solution on YOUR website!
X = amount won (before the cost is factored in)
X either equals 58 or 0
H = heads
T = tails
Sample space = {HH, HT, TH, TT} = set of all possible outcomes
Event space = {HH} = subset of the sample space in which the player wins
If the player gets the result in the event space, then they win.
P(winning) = (1 item in the event space)/(4 items in sample space)
P(winning) = 1/4 = 0.25
P(losing) = 1-P(winning) = 1-0.25 = 0.75
| Event | X | P(X) | X*P(X) | | Win | 58 | 0.25 | 14.5 | | Lose | 0 | 0.75 | 0 |
E[X] = expected value
E[X] = sum of the X*P(X) values
E[X] = 14.5 + 0
E[X] = 14.5
The expected winnings is 14.5 cents per game.
This is before the cost is factored in.
To have a fair game, the cost per game must be the same as the amount expected to win per game.
The fair price per game is 14.5 cents
For 2 games, that cost will be 2*14.5 = 29 cents.
---------------------------------------------------------
Another approach
c = cost to play one game
X = net winnings
In this scenario, X is the amount of money the player walks away with after the cost is factored in.
The player walks away with 58-c cents if they won, or they walk away with 0-c = -c cents if they lose (i.e. they lose c cents).
| Event | X | P(X) | X*P(X) | | Win | 58-c | 0.25 | (58-c)*0.25 = 0.25*58-0.25c= 14.5-0.25c | | Lose | -c | 0.75 | -c*0.75 = -0.75*c |
E[X] = sum of the X*P(X) values
E[X] = ( 14.5-0.25c ) + ( -0.75c )
E[X] = 14.5 - c
To have a fair game, the expected net winnings must be 0
E[X] = 0
14.5 - c = 0
14.5 = c
c = 14.5
It should cost 14.5 cents to play the game once, if we wanted a fair game.
Therefore, 2 games should cost 2*14.5 = 29 cents.
Answer by ikleyn(52781)  (Show Source):
You can put this solution on YOUR website! .
A game involving tossing 2 coins and receiving 58 cents if they are both heads.
What is a fair price to pay for the privilege of playing this game twice?
~~~~~~~~~~~~~~
The probability to win in each game is 1/4 = 0.25.
The fair price to play this game once is 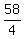 =  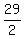= 14.5 cents.
The fair price to play this game twice is 2*14.5 cents = 29 cents. ANSWER
Solved and explained.
////////////////
The answer in the post by @MathLover1 is incorrect.
|
|
|
