Question 1197229: rooms 1 2 3 4 5 6 7 8+
47 140 1170 2350 2450 2130 1370 1560 (# of units in thousands)
The table above provides information on housing units in some part of the U.S.
Consider the following five events:
A = the unit has at most four rooms
B = the unit has at least two rooms
C = the unit has between five and seven rooms inclusive
D = the unit has more than seven rooms
E = the unit has less than three rooms
Determine the NUMBER OF OUTCOMES (in thousands) that comprise each event given below.
(a) A or C:
(b) B and C:
(c) not B:
(d) not C:
(e) B and E:
Answer by math_tutor2020(3820)   (Show Source): (Show Source):
You can put this solution on YOUR website!
| # of rooms | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8+ | | # of units (in thousands) | 47 | 140 | 1170 | 2350 | 2450 | 2130 | 1370 | 1560 |
For instance, we have 47 thousand units with 1 room
Another example: there are 140 thousand units with 2 rooms.
===============================================================
Part (a)
Events to focus on
A = the unit has at most four rooms
C = the unit has between five and seven rooms inclusive
n(A) = number of units having at most four rooms
n(A) = number of units having 1,2,3,or 4 rooms
n(A) = (# units w/ 1 room)+(# units w/ 2 rooms)+(# units w/ 3 rooms)+(# units w/ 4 rooms)
n(A) = (140 thousand)+(1170 thousand)+(2350 thousand)+(2450 thousand)
n(A) = 6110 thousand
n(A) = 6110*1000
n(A) = 6,110,000
n(C) = number of units having between 5 and 7 rooms inclusive
n(C) = (# units w/ 5 rooms)+(# units w/ 6 rooms)+(# units w/ 7 rooms)
n(C) = (2450 thousand)+(2130 thousand)+(1370 thousand)
n(C) = 5950 thousand
n(C) = 5950*1000
n(C) = 5,950,000
n(A and C) = number of units having at most 4 rooms AND between 5 and 7 rooms
n(A and C) = 0
The events "at most 4" and "between 5 and 7" have no overlap
Draw a number line if needed to be able to see why there isn't an overlap.
It's impossible for events A and C to happen simultaneously
We consider these two events mutually exclusive.
n(A or C) = n(A) + n(C) - n(A and C)
n(A or C) = 6,110,000 + 5,950,000 - 0
n(A or C) = 12,060,000
Answer: 12,060,000
This is slightly over 12 million
===============================================================
Part (b)
Events to focus on
B = the unit has at least two rooms
C = the unit has between five and seven rooms inclusive
Event C is a subset of event B, so to speak.
Draw out a number line. Mark 2, 5 and 7 on the number line.
In red, shade  for event B for event B
In blue, shade  for event C for event C
The overlapping region in purple is  which is in common to BOTH event B and event C. which is in common to BOTH event B and event C.
Therefore,
n(B and C) = n(C) = 5,950,000
Answer: 5,950,000
A little short of 6 million.
===============================================================
Part (c)
B = the unit has at least two rooms
n(B) = number of units with at least 2 rooms
n(B) = number of units with 2 rooms or more (i.e. 2,3,4,...)
n(B) = (# of units w/ 2 rooms)+(# of units w/ 3 rooms)+...+(# of units with 8 rooms or more)
not B = the unit does not have at least two rooms
not B = the unit has 1 room
Events "B" and "not B" are complete opposites of each other.
Search out "complementary events" for more information.
n(not B) = number of units with 1 room exactly
n(not B) = 47 thousand = 47,000
Answer: 47,000
===============================================================
Part (d)
C = the unit has between five and seven rooms inclusive
n(C) = number of units having between 5 and 7 rooms inclusive
n(C) = (# units w/ 5 rooms)+(# units w/ 6 rooms)+(# units w/ 7 rooms)
n(C) = (2450 thousand)+(2130 thousand)+(1370 thousand)
n(C) = 5950 thousand
n(C) = 5950*1000
n(C) = 5,950,000
Refer to part (a) where this was brought up earlier.
Event "not C" is the opposite of event "C". These events are complementary.
See the previous section part (c) for a similar situation.
not C = unit does not have 5, nor 6, nor 7 rooms
not C = unit has 1,2,3,4,8,9,10,... rooms
n(not C) = total - n(C)
n(not C) = (11217 thousand) - (5950 thousand)
n(not C) = (11217 thousand) - (5950 thousand)
n(not C) = 5267 thousand
n(not C) = 5267*1000
n(not C) = 5,267,000
note: The "total" refers to adding up everything in the bottom row of the given table.
n(C)+n(not C) = total
Answer: 5,267,000
Slightly over 5.2 million
===============================================================
Part (e)
We'll focus on these events
B = the unit has at least two rooms
E = the unit has less than three rooms
Draw out a number line
 represents event B represents event B
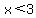 is event E is event E
The overlap is the interval 
If x is an integer, then we're simply talking about the single x value x = 2
In other words "2 rooms" fits the criteria of "at least 2" and "less than 3" applied simultaneously.
The table shows 140 thousand for the number of units with 2 rooms.
140 thousand = 140 *1000 = 140,000
Answer: 140,000
|
|
|