SOLUTION: There are 15 glass vases sold in an antique shop and 6 of them are slightly cracked. What is the chance that when a customer buys 5 vases 3 of them will be cracked?

Algebra ->  Probability-and-statistics -> SOLUTION: There are 15 glass vases sold in an antique shop and 6 of them are slightly cracked. What is the chance that when a customer buys 5 vases 3 of them will be cracked?      Log On


   

Question 1195012: There are 15 glass vases sold in an antique shop and 6 of them are slightly cracked. What is the chance that when a customer buys 5 vases 3 of them will be cracked?
Answer by ikleyn(52776) About Me  (Show Source):
You can put this solution on YOUR website!
.
There are 15 glass vases sold in an antique shop and 6 of them are slightly cracked.
What is the chance that when a customer buys 5 vases 3 of them will be cracked?
~~~~~~~~~~~~~~~~ 

Of 15 glass vases, 6 are cracked and 15-6 = 9 are not.


To answer the question, we should calculate the number of all possible 5-vase subsets 
in the set of 15 vases, and then relate it to the number of all possible subsets
of 5 vases, comprising of 3 cracked and 2 good vases.


The number of all possible 5-vase subsets in the set of 15 vases is 

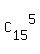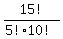    C%5B15%5D%5E5 = 15%21%2F%285%21%2A10%21%29 = %2815%2A14%2A13%2A12%2A11%29%2F%281%2A2%2A3%2A4%2A5%29 = 3003.


The number of all possible 5-vase subsets comprising of 3 cracked and 2 good vases is

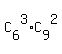    C%5B6%5D%5E3%2AC%5B9%5D%5E2 = 20*36 = 720.


Therefore, the sough probability is  

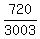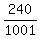    P = favorable%2Ftotal = 720%2F3003 = 240%2F1001 = 0.23976  (rounded).    ANSWER

Solved.