.
A certain virus infects one in 400 people. A test used to detect the virus in a person is positive
90% of the time if the person has the virus and 8% of the time if the person does not have the virus.
Let A be the event the person is infected and B be the event the person tests positive.
Find the probability that a person has the virus given that they have tested positive (find P(A/B).
Round your answer to the nearest tenth of a percent and do not include a percent sign
~~~~~~~~~~~~~~~~
Let the entire population will be 40000 persons.
Then 1/400 are infected, i.e.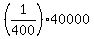 
= 100 persons.
Of these 100 persons, 90% are test positive, i.e. 90 persons.
These 90 are infected and test positive, at the same time; so, these 90 are the intersection of events A and B;
therefore, the numerator of the fraction in the formula for the conditional probability is 90.
Next, among the rest 40000-100 = 39900 healthy persons, 8%, or 0.08*39900 = 3192 are test positive.
So, the total test positive is 90 + 3192 = 3282 persons.
Thus, event B has 3292 persons: this number is the denominator of the fraction for the conditional probability.
After these explanations, the conditional probability P(A|B) is
P(A|B) = 
= 
= 0.027422 = 0.027 (rounded) = 2.7 %. ANSWER
Solved.
