SOLUTION: There are three sets of traffic lights on Zimmer’s journey to work. The independent probabilities that Zimmer has to stop at the first, second and third sets of lights are 0.4, 0

Click here to see ALL problems on Probability-and-statistics

Question 1193151: There are three sets of traffic lights on Zimmer’s journey to work. The independent probabilities that Zimmer has to stop at the first, second and third sets of lights are 0.4, 0.8 and 0.3 respectively.
a) Draw a tree diagram to show this information.
b) Find the probability that Zimmer has to stop at the first and third sets of lights but
does not have to stop at the second set.
c) Find the probability that Zimmer has to stop at exactly two of the three sets of lights.
d) Find the probability that Zimmer has to stop at the second set of lights, given that he
has to stop at exactly two sets of lights.

I have done a and b, however stuck on c and d...
Answer by ikleyn(52777)   (Show Source):
You can put this solution on YOUR website!
.

                    Solution to part (c)

P = P(stop1 stop2 no-stop3) + P(stop1 no-stop2 stop3) + P(no-stop1 stop2 stop3) = = 0.4*0.8*(1-0.3) + 0.4*(1-0.8)*0.3) + (1-0.4)*0.8*0.3 = 0.392 (exact value). ANSWER

                    Solution to part (d)

It is the conditional probability P = . The denominator is the probability that Zimmer will stop at exactly two lights: we just found this expression and the value 0.392 in part (c). The numerator is, OBVIOULSY, = P(stop1 stop2 no-stop3) + P(no-stop1 stop2 stop3) = = 0.4*0.8*(1-0.3) + (1-0.4)*0.8*0.3 = 0.368 (exact value). Now the ANSWER to this question is P = = = 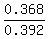0.9388 (rounded).

Solved.