Question 1191726: Connecticut Lottery In the Cash Five Lottery in Connecticut, a player pays 1 dollar for a single ticket with five numbers. Five balls numbered 1 through 35 are randomly chosen from a bin without replacement. If all five numbers on a player's ticket match the five chosen, the player wins 100,000 dollars. The probability of this occurring is 1/(324,632) If four numbers match, the player wins 300 dollars This occurs with probability 1/2164 If three numbers match, the player wins 10 dollars This occurs with probability 1/75 . Compute and interpret the expected value of the game from the player's point of view.
Answer by ikleyn(52946)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Connecticut Lottery In the Cash Five Lottery in Connecticut, a player pays 1 dollar
for a single ticket with five numbers. Five balls numbered 1 through 35 are randomly
chosen from a bin without replacement. If all five numbers on a player's ticket match
the five chosen, the player wins 100,000 dollars. The probability of this occurring
is 1/(324,632) If four numbers match, the player wins 300 dollars
This occurs with probability 1/2164 If three numbers match, the player wins 10 dollars
This occurs with probability 1/75 .
Compute and interpret the expected value of the game from the player's point of view.
~~~~~~~~~~~~~~~~~~
Actually, the probabilities to match four numbers or three numbers are DIFFERENT
from that shown in the problem's formulation.
The probability to match 4 (four) numbers (if the order does not matter) is
P(4) =  = = 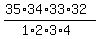 = = 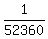 ;
The probability to match 3 (three) numbers (if the order does not matter) is
P(3) = ;
The probability to match 3 (three) numbers (if the order does not matter) is
P(3) =  = = 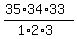 = =  .
The probability to match 5 numbers is as shown in the post. .
The probability to match 5 numbers is as shown in the post.
-----------
So, the problem's formulation is EITHER incorrect OR should be explained in more details.
With the given data, the game expectation is
E = 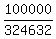 + + 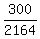 + + 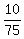 - -  = -0.42. = -0.42.
It means that a player loses 42 cents in each game's ticket, in average.
It is so UNFAIRE game expectation that no one state regulator will allow such lottery.
|
|
|