SOLUTION: A box contains 7 identical marbles, except for color, of which 4 are red and 3 are green. Two marbles are selected at random (a) one by one with replacement; (b) one by one witho

Algebra ->  Probability-and-statistics -> SOLUTION: A box contains 7 identical marbles, except for color, of which 4 are red and 3 are green. Two marbles are selected at random (a) one by one with replacement; (b) one by one witho      Log On


   

Question 1191169: A box contains 7 identical marbles, except for color, of which 4 are red and 3 are green. Two
marbles are selected at random (a) one by one with replacement; (b) one by one without
replacement; (c) two marbles together.
Compute the numbers of sample points in all these cases
Answer by ikleyn(52781) About Me  (Show Source):
You can put this solution on YOUR website!
A box contains 7 identical marbles, except for color, of which 4 are red and 3 are green.
Two marbles are selected at random (a) one by one with replacement; (b) one by one without
replacement; (c) two marbles together.
Compute the numbers of sample points in all these cases
~~~~~~~~~~~~~~~


Part  (c)  is  IDENTICAL  to part  (b).   THEREFORE,  there is no sense to consider part  (c)  separately,

and I will not consider part  (c)  separately.   It is covered by part  (b),  in full.


                Part  (a) 

The sample space consists of 4 elements  RR, RG, GR, GG with the probabilities

    P(RR) = 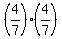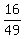%284%2F7%29%2A%284%2F7%29 = 16%2F49;

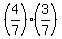    P(RG) = %284%2F7%29%2A%283%2F7%29 = 12%2F49%29;

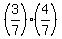    P(GR) = %283%2F7%29%2A%284%2F7%29 = 12%2F49;

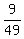    P(GG) = %283%2F7%29%2A%283%2F7%29 = 9%2F49

with the total sum  P((RR) + P(RG) + P(GR) + P(GG) = 1.

Part  (a)  is complete.


                Part  (b) 

The sample space consists of 4 elements  RR, RG, GR, GG with the probabilities

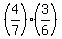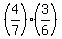    P(RR) = %284%2F7%29%2A%283%2F6%29 = 2%2F7;

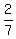    P(RG) = %284%2F7%29%2A%283%2F6%29 = 2%2F7%29;

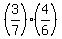    P(GR) = %283%2F7%29%2A%284%2F6%29 = 2%2F7;

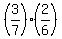    P(GG) = %283%2F7%29%2A%282%2F6%29 = 1%2F7

with the total sum  P((RR) + P(RG) + P(GR) + P(GG) = 1.

Part  (b)  is complete.


The problem is solved,  in full.