Question 119092: pls answer this question for me..
" if an experiment consist of tossing a die once and drawing 2 balls in succession w/ replacement if the outcome in the die is a prime number, otherwise balls are drawn w/o replacement.
(note: 1 is not a prime number; the urn contains 2 red and 1 black balls)
find the probability that:
a. the balls are drawn w/o replacement.
b. ball drawn include at least 1 red ball in (w/ replacement, w/o replacement).
c. the balls drawn are of different colors in(w/ replacement, w/o replacement).
d. the ball drawn are both black given that the outcome in the die is prime in
(w/ replacement, w/o replacement).
please help me answer this problem.. a million thanks!
Answer by solver91311(24713)   (Show Source):
You can put this solution on YOUR website! Part a.
The balls are drawn without replacement if the result on the die is not prime. The die has 6 numbers, 1, 2, 3, 4, 5, and 6. Of these, three numbers are prime and three are not. So the probability that the balls would be drawn without replacement is  or 
Part b.
Calculating the probability of at least one red ball being drawn with or without replacement is comparitively difficult. Easier is to calculate the probability that both balls will be black and subtract that from 1.
Without replacement: The probability that the first ball drawn will be black given 2 red balls and 1 black balls is  . Since the first draw will not be replaced, the probability of drawing a second black ball is 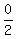 because, given that the first draw was black, the there are only two balls left and both of them are red. These are independent probabilities, meaning that the outcome of the second draw does not depend on the outcome of the first draw, so the total probability is the product of the individual probabilities, that is:  . Therefore, there is 0 probability that two black balls would be drawn given no replacement so the probability that at least one of the balls is red is  or certainty.
With replacement: Again, calculate the probability that both balls drawn will be black. The probability that the first ball drawn is black is again , but since we are replacing the drawn ball, the probability that the second ball will be black is still . Again, we have independent probabilities, so the total is the product  . That means that the probability that at least one of the balls is red is 
Part c.
Without replacement. We need the probability that the balls drawn are of different colors. This is 1 minus the probability that they are the same color. We have already calculated the probability that both balls would be black if drawn without replacement, and that is 0. The probability that both balls would be red is  for the first draw and for the second draw and the total probability for both being red  . So the probability that both will be black OR both will be red is  . That means that the probability that you will draw two different colors is  .
With replacement. Similar to the above. Probability of two reds:  . Probability of two blacks: (from Part b)  . Probability of two reds OR two blacks:  . Finally the probability of two different colors: 
Part d.
Probability that both are black given the die result is prime, i.e., the balls will be drawn with replacement. See the 'With Replacement' part of part b. The probability is
Hope this helps,
John
|
|
|
