Question 1183791: Two people A and B are to draw alternately one ball at a time from an urn containing 3 white and 2 black balls, drawn balls not being replaced. If A takes the first turn, what is the probability that A will be the first to draw white?
Found 2 solutions by Theo, ikleyn:
Answer by Theo(13342)   (Show Source): (Show Source):
You can put this solution on YOUR website! i believe the probability that A draws a white ball first is .7.
my thinking:
A gets the white ball on the first draw.
that probability is 3/5 = .6
A gets the white ball on the second draw.
in order for this to happen, both A and B must have drawn a black ball on their first try..
if they do, then there are only white balls left and A is sure to draw a white ball on his second try.
the probability of this happening is 2/5 * 1/4 * 3/3 = 6/60 = .1.
the probability that A is first to get a white ball is therefore .6 + .1 = .7.
since the total probability must be equal to 1, then the probability that B gets the white ball first must be .3.
the ways that this could happen are:
B draws a white ball on the first try.
in order for this to happen, A must have drawn a black ball on the first try.
the probability that B is the first to draw a white ball on the first try is therefore 2/5 * 3/4 = 6/20 = .3
B draws a white ball first on the second try.
in order for this to happen, both A and B must have drawn a black ball on their first try.
sine there are only white balls left, then A is assured to get a white ball on the second try.
the probability that B gets a white ball on the second try is therefore 0.
the probabilities seem to be true.
the probability that A gets a white ball first is .7
the probability that B gets a white ball first is .3
the total probabilities are equal to 1.
this seems reasonable, which is why i think the probability that A gets a white ball first is .7.
Answer by ikleyn(52756)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Two  persons A and B are to draw alternately one ball at a time from an urn containing 3 white and 2 black balls, persons A and B are to draw alternately one ball at a time from an urn containing 3 white and 2 black balls,
drawn balls not being replaced. If A takes the first turn, what is the probability that A will be the first to draw white ?
~~~~~~~~~~~~~~~
We may think about the space of events as all possible sequences of the letters W and B of the length 5.
There are 120 permutations of 5 items; but if we consider the distinguishable arrangements of these sequences,
we have only  = = 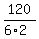 = =  = 10 distinguishable orderings, so the space of events has 10 elements.
Next, the "favorable" arrangements are those that EITHER start from W (and then A takes white ball first),
OR those that start from BBW (and then there is only one such sequence BBWWW, where, again, A takes white ball first).
The number of distinguishable sequences W _ _ _ _ is = 10 distinguishable orderings, so the space of events has 10 elements.
Next, the "favorable" arrangements are those that EITHER start from W (and then A takes white ball first),
OR those that start from BBW (and then there is only one such sequence BBWWW, where, again, A takes white ball first).
The number of distinguishable sequences W _ _ _ _ is  = =  = 6.
The sequence BBWWW is a unique of that kind.
So, the number of favorable distinguishable sequences is (6+1) = 7, and the total space of events has 10 elements.
THEREFORE, the probability under the problem's question is P = = 6.
The sequence BBWWW is a unique of that kind.
So, the number of favorable distinguishable sequences is (6+1) = 7, and the total space of events has 10 elements.
THEREFORE, the probability under the problem's question is P =  = = 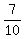 = 0.7 = 70%. ANSWER = 0.7 = 70%. ANSWER
Solved.
------------------
Good problem (!)
I like it (!)
|
|
|