.
A student has 12 classmates.
(a) In how many combinations can she invite five of them to lunch?
(b) Two classmates are having a dispute and refuse to be together.
In how many combinations can she invite five classmates if these two are not together?
~~~~~~~~~~~~~~~~~~
Part (a)
There are 
= 
= 
= 
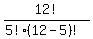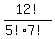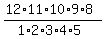= 792 such combinations. ANSWER
Part (b)
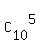combinations of five, where NEITHER classmate A NOR classmate B present (the selection is 5 from 10), P L U S
combinations of four (+ A), where classmate A does present, but classmate B does not (the selection is 4 from 10), P L U S
combinations of four (+ B), where classmate A does not present, but classmate B does (the selection is 4 from 10).
In all, there are +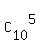 
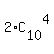= 252 + 2*210 = 672 such combinations. ANSWER
It can be computed by different way as - 
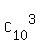= 792 - 120 = 672 (giving the same answer),
taking all possible combinations of 5 from 12 and subtracting all combinations of 5 from 12, that include both disputed classmates.
+-----------------------------------------------------------------------+
| CONSIDER this parallel computing AS a GOOD and a NECESSARY CHECK |
+-----------------------------------------------------------------------+
Solved.
/////////////
On Combinations, see introductory lessons
- Introduction to Combinations
- PROOF of the formula on the number of Combinations
- Problems on Combinations
- Problems on Combinations with restrictions
in this site.
Also, you have this free of charge online textbook in ALGEBRA-II in this site
- ALGEBRA-II - YOUR ONLINE TEXTBOOK.
The referred lessons are the part of this online textbook under the topic "Combinatorics: Combinations and permutations".
Save the link to this textbook together with its description
Free of charge online textbook in ALGEBRA-II
https://www.algebra.com/algebra/homework/complex/ALGEBRA-II-YOUR-ONLINE-TEXTBOOK.lesson
into your archive and use when it is needed.
