Question 1182548: Three airlines serve a small town in Rajkot District. Airline A has 50% of all the scheduled
flights, airline B has 30%, and airline C has the remaining 20%. Their on-time rates are 80%, 65%, and 40%, respectively. A plane has just left on time. What is the probability that it was airline A?
Note: Draw the Tree-diagram using Paint App
Answer by ikleyn(52848)   (Show Source):
You can put this solution on YOUR website! .
Three airlines serve a small town in Rajkot District. Airline A has 50% of all the scheduled
flights, airline B has 30%, and airline C has the remaining 20%. Their on-time rates are 80%, 65%, and 40%, respectively.
A plane has just left on time. What is the probability that it was airline A?
Note: Draw the Tree-diagram using Paint App
~~~~~~~~~~~~~~~~~~~~~~~
Let x be the total number of flights.
Then airline A provides 0.5x flights; airline B provides 0.3x flights and airline C provides the remaining 0.2x flights.
Notice that in total 0.5x + 0.3x + 0.2x = x.
The amount of on-time flights by airline A is 0.8*(0.5x); by airline B is 0.65*(0.3x), and by airline C is 0.4*(0.2x).
The total number of flights on-time by airlines A, B and C together is Total_on_time = 0.8*(0.5x) + 0.65*(0.3x) + 0.4*(0.2x).
The problem's question is about the CONDITIONAL probability P(the flight is by A | the flight is on-time).
By the definition of the conditional probability,
P(the flight is by A | the flight is on-time) = 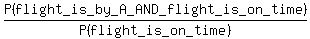 . (1)
The numerator of this fraction is 0.4*(0.2x), as explained above.
The denominator is 0.8*(0.5x) + 0.65*(0.3x) + 0.4*(0.2x), due to the same reason.
So the probability under the problem's question is
P = 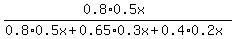 = cancel x in the numerator and denominator and continue =
=  = now apply your calculator = 0.5926 (rounded) = 59.26%. ANSWER
Solved.
------------
Post-solution notes and the lessons to learn
(1) The major lessons to learn from my solutions are
(a) the logic of the solution
(b) the structure of the final formula
(c) the way HOW I get the formula via the definition of the CONDITIONAL probability.
(d) If you learn this method of solution, then after some practice, you will be able to solve similar problems
in a semi-automatic mode, writing the final calculation formula immediately without intermediate explanations.
(2) You do not need the tree-diagram - you need understand the logic of the solution.
If you want, you can make the diagram on your own for yourself.
(3) Please keep in your mind that this forum IS NOT an art-studio to make plots for you on your request.
----------------
One technical note in conclusion.
Notice that I do not make intermediate calculations on the way: additions or multiplications.
My goal at the solution process is to combine and to write the standard calculation formula as it should be in its full form.
As soon as it is done, I copy-paste the formula into Excel spreadsheet and get the numerical answer in one click and with no errors.
It is an important part of the whole technology.
----------------
At this point, I complete my teaching.
Do not forget to post your "THANKS" to me.
|
|
|
