Question 1176467: An elementary school is offering 3 language classes: one in Spanish, one in French, and one in German. These classes are open to any of the 89 students in the school. There are 37 in the Spanish class, 37 in the French class, and 21 in the German class. There are 17 students that in both Spanish and French, 7 are in both Spanish and German, and 8 are in both French and German. In addition, there are 4 students taking all 3 classes.
a)If one student is chosen randomly, what is the probability that he or she is taking exactly two language classes?
Answer:20/89
b)If two students are chosen randomly, what is the probability that neither of them is taking a language class?
Answer by ikleyn(52794)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
An elementary school is offering 3 language classes: one in Spanish, one in French, and one in German.
These classes are open to any of the 89 students in the school.
There are 37 in the Spanish class, 37 in the French class, and 21 in the German class.
There are 17 students that in both Spanish and French, 7 are in both Spanish and German,
and 8 are in both French and German.
In addition, there are 4 students taking all 3 classes.
a)If one student is chosen randomly, what is the probability that he or she is taking exactly two language classes?
Answer:20/89
b)If two students are chosen randomly, what is the probability that neither of them is taking a language class?
~~~~~~~~~~~~~~~~~~~~~
PART (a)
Probability (Spanish and French only, but no German)
P(S and F only) = P((S and F) but not G) =  = = 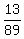 .
Probability (Spanish and Germain only, but no French)
P(S and G only) = P((S and G) but not F) = .
Probability (Spanish and Germain only, but no French)
P(S and G only) = P((S and G) but not F) = 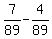 = = 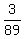 .
Probability (French and Germain only, but no Spanish)
P(F and G only) = P((F and G) but not S) = .
Probability (French and Germain only, but no Spanish)
P(F and G only) = P((F and G) but not S) = 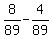 = = 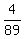 .
Finally, the probability under the problem's question is this sum
P(taking EXACTLY two language classes) = P(S and F only) + P(S and G only) + P(F and G only) = .
Finally, the probability under the problem's question is this sum
P(taking EXACTLY two language classes) = P(S and F only) + P(S and G only) + P(F and G only) = 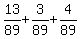 = = 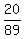 . ANSWER . ANSWER
PART (b)
We calculate first the probability that the randomly chosen student takes at least one Language class.
For it, use the inclusion-exclusion formula for the probability of the combined event ( S U F U G )
P(S U F U G) = P(S) + P(F) + P(G) - P(SF) - P(SG) - P(SG) + P(SFG) =
= 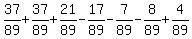 =
= =
= 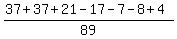 = = 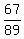 .
Then the answer to part (b) is the COMPLEMENT to it, i.e.
P(case b) = 1 - .
Then the answer to part (b) is the COMPLEMENT to it, i.e.
P(case b) = 1 - 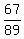 = = 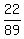 . ANSWER . ANSWER
The problem is solved --- all questions are answered.
Solved, answered, explained and completed.
|
|
|