Question 1174578: A family has five children. Assuming that the probability of a girl on each birth was 0.5 and
that the five births were independent,
what is the probability the family has at least one girl, given that they have at least one boy?
Answer by ikleyn(52781)   (Show Source):
You can put this solution on YOUR website! .
A family has five children. Assuming that the probability of a girl on each birth was 0.5
and that the five births were independent,
what is the probability the family has at least one girl, given that they have at least one boy?
~~~~~~~~~~~~~~~~~~~
As it is well known fact, in all, there are  = 32 possible configurations / elements
in the space of events, each case with the probability of  .
Since the condition is imposed "there is at least one boy", we exclude this singular case
of having all 5 girls in the family.
So, the reduced space of events consists now of 32-1 = 31 configurations, with "all 5 girls" excluded.
Therefore, the number 31 is the reduced cardinality of the total space of events: "total reduced" = 31.
The problem asks about configurations, in which there is at least one girl - so the case "all 5 boys" is excluded.
It reduces the number of "favorable" cases from 31 to 31-1 = 30.
THEREFORE, the probability under the problem's question is P =  . ANSWER
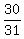ANSWER. The probability is .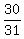
Solved.
|
|
|
