Question 1170818: There are no equations given, I'm not sure where to start or how to prove this.
A company claims to have invented a device that can measure the momentum of objects inside it with extreme
accuracy. The device fits within a matchbox, and the claimed precision with which it can measure momentum is
δp = ±10^−26kg ms^−1
.
Explain why the claimed performance cannot possibly be accurate, and estimate the smallest possible size of a
device with such momentum precision, according to laws of quantum physics.
Found 2 solutions by CPhill, ikleyn:
Answer by CPhill(1959)   (Show Source): (Show Source):
You can put this solution on YOUR website! Let's break down why this claim violates the principles of quantum physics, specifically the Heisenberg Uncertainty Principle.
**1. Heisenberg Uncertainty Principle**
The Heisenberg Uncertainty Principle states that there is a fundamental limit to the precision with which certain pairs of physical properties of a particle can be known simultaneously. In this case, the relevant pair is position (Δx) and momentum (Δp).
The principle is expressed as:
Δx Δp ≥ ħ/2
where:
* Δx is the uncertainty in position.
* Δp is the uncertainty in momentum.
* ħ (h-bar) is the reduced Planck constant, approximately 1.054 × 10⁻³⁴ J s.
**2. Why the Claim Violates the Principle**
The company claims a momentum precision of:
Δp = 10⁻²⁶ kg m/s
Let's use the Heisenberg Uncertainty Principle to calculate the minimum uncertainty in position (Δx) for this momentum precision:
Δx ≥ ħ / (2Δp)
Δx ≥ (1.054 × 10⁻³⁴ J s) / (2 × 10⁻²⁶ kg m/s)
Δx ≥ 0.527 × 10⁻⁸ meters
Δx ≥ 5.27 × 10⁻⁹ meters
Δx ≥ 5.27 nanometers
This result means that if the momentum of an object is measured with a precision of 10⁻²⁶ kg m/s, the minimum uncertainty in the object's position would be approximately 5.27 nanometers.
**3. The Contradiction**
The company claims the device fits within a matchbox. A typical matchbox has dimensions on the order of centimeters (10⁻² meters).
The uncertainty in position (5.27 nanometers or 5.27 × 10⁻⁹ meters) is far smaller than the size of the matchbox (10⁻² meters). This means that to achieve the claimed momentum precision, the position of the object would have to be known to a much higher degree of accuracy than the size of the device it's contained within.
**4. Estimating the Smallest Possible Size**
To find the smallest possible size of a device that could accommodate the claimed momentum precision, we need to consider the uncertainty in position. The uncertainty in position (Δx) must be at least as large as the size of the device.
Let's assume the device has a size comparable to the uncertainty in position:
Δx ≈ 5.27 × 10⁻⁹ meters
This means the smallest possible size of the device would need to be on the order of nanometers. This is far smaller than a matchbox.
**Conclusion**
The company's claim is impossible because:
* The Heisenberg Uncertainty Principle dictates that there is a fundamental limit to the precision with which position and momentum can be known simultaneously.
* Achieving the claimed momentum precision would require the object's position to be known with an uncertainty much smaller than the size of a matchbox.
* The smallest possible size of a device with such momentum precision would be on the order of nanometers, not centimeters.
Answer by ikleyn(52776)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
There are no equations given, I'm not sure where to start or how to prove this.
A company claims to have invented a device that can measure the momentum of objects inside it with extreme
accuracy. The device fits within a matchbox, and the claimed precision with which it can measure momentum is
δp = ±10^−26kg ms^−1
.
Explain why the claimed performance cannot possibly be accurate, and estimate the smallest possible size of a
device with such momentum precision, according to laws of quantum physics.
~~~~~~~~~~~~~~~~~~~~~~~~~
In this post, the problem is posed in wrong way, so it is either
a EXTREME stupidity, or an EROOR, or a trap (like a provocation).
From the uncertainty principle, the uncertainty in determining the position is
Δx ≥ 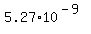 meters.
This uncertainty is MUCH-MUCH-much-much less that the size of a matchbox.
THEREFORE, in this problem, the uncertainty principle of the quantum mechanics
PROHIBITS for the device to have the size less than meters.
This uncertainty is MUCH-MUCH-much-much less that the size of a matchbox.
THEREFORE, in this problem, the uncertainty principle of the quantum mechanics
PROHIBITS for the device to have the size less than 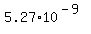 meters,
but DOES NOT prohibit for the device to have a greater size, like a matchbox.
HENCE, as a CONCLUSION, a device in this problem, which provides the given precision,
EASILY may have a size of a matchbox - nothing from quantum mechanics prevents it. meters,
but DOES NOT prohibit for the device to have a greater size, like a matchbox.
HENCE, as a CONCLUSION, a device in this problem, which provides the given precision,
EASILY may have a size of a matchbox - nothing from quantum mechanics prevents it.
In his post, @CPhill puffs out his cheeks and tries to play a role of an expert.
He uses a lot of words and tries to obfuscate the question, but does not give a direct answer.
So, for the safety of your mind, IGNORE the post by @CPhill.
Also, ignore the problem itself, since it is posed in WRONG WAY.
\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\
Regarding the post by @CPhill . . .
Keep in mind that @CPhill is a pseudonym for the Google artificial intelligence.
The artificial intelligence is like a baby now. It is in the experimental stage
of development and can make mistakes and produce nonsense without any embarrassment.
It has no feeling of shame - it is shameless.
This time, again, it made an error.
Although the @CPhill' solution are copy-paste Google AI solutions, there is one essential difference.
Every time, Google AI makes a note at the end of its solutions that Google AI is experimental
and can make errors/mistakes.
All @CPhill' solutions are copy-paste of Google AI solutions, with one difference:
@PChill never makes this notice and never says that his solutions are copy-past that of Google.
So, he NEVER SAYS TRUTH.
Every time, @CPhill embarrassed to tell the truth.
But I am not embarrassing to tell the truth, as it is my duty at this forum.
And the last my comment.
When you obtain such posts from @CPhill, remember, that NOBODY is responsible for their correctness,
until the specialists and experts will check and confirm their correctness.
Without it, their reliability is ZERO and their creadability is ZERO, too.
|
|
|