Question 1168713: Scientific research on popular beverages consisted of 60 studies that were fully sponsored by the food industry, and 40 studies that were conducted with no corporate ties. Of those that were fully sponsored by the food industry, 15 % of the participants found the products unfavorable, 23 % were neutral, and 62 % found the products favorable. Of those that had no industry funding, 38 % found the products unfavorable, 15 % were neutral, and 47 % found the products favorable.
a)What is the probability that a participant selected at random found the products favorable?
b)If a randomly selected participant found the product favorable, what is the probability that the study was sponsored by the food industry?
If a randomly selected participant found the product unfavorable, what is the probability that the study had no industry funding?
Answer by ikleyn(52781)   (Show Source):
You can put this solution on YOUR website! .
In order for the problem could be clearly solved, the condition should be presented in clearly structured form,
as I did it below.
Questions ALSO should be clearly marked, as I did it in my versions below.
~~~~~~~ The condition in edited/structured form START ~~~~~~~~~~~
Scientific research on popular beverages consisted of 60 studies that were fully sponsored by the food industry,
and 40 studies that were conducted with no corporate ties.
Of those that were fully sponsored by the food industry, 15 % of the participants found the products unfavorable,
23 % were neutral, and
62 % found the products favorable.
Of those that had no industry funding, 38 % found the products unfavorable,
15 % were neutral, and
47 % found the products favorable.
a) What is the probability that a participant selected at random found the products favorable?
b) If a randomly selected participant found the product favorable, what is the probability
that the study was sponsored by the food industry?
(c) If a randomly selected participant found the product unfavorable, what is the probability that the study had no industry funding?
~~~~~~~ The condition in edited/structured form END ~~~~~~~~~~~
Solution
Even better it would be to present the condition in the form of the Table, using short keywords for the rows and the columns.
Start the solution noticing that partial probabilities sum up to 100%:
15% + 23% + 62% = 100%; 38% + 15% + 47% = 100%
Now I am ready answer the questions.
I will give the answers as self-explanatory formulas, leaving it to you to complete simple calculations on your own.
(a) P = 0.6*0.62 + 0.4*0.47.
(b) P =  ,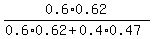
The question is about the conditional probability, and the answer is the formula
related to the conditional probability.
(c) P =  .
The question is about the conditional probability, and the answer is the formula
related to the relevant conditional probability.
-----------
My solution is completed
As I said, the formulas are self-explanatory.
If you have question, look in these formulas attentively and listen what they tell you.
You can also post your questions to me directly.
|
|
|
