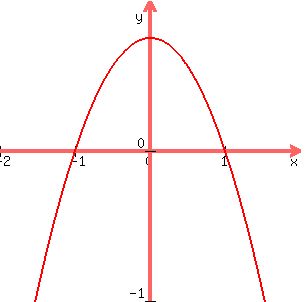
Question 1168707: A random variable X has pdf f(x) = (3/4)(1-x^2) from -1 < x < 1.
1. Find the cdf
2. Find the first, second and third quartiles.
I have found that the cdf = F(x) = -(x^3)/4 + 3x/4
by taking the integral of f(t) = (3/4)(1-t^2) from [-1,x]
From there I know I need to solve for F(x) = 0.25, F(x) = 0.5 and F(x) = 0.75. However when I solve for those, I keep getting values outside of the interval [-1,1].
Found 2 solutions by Boreal, ikleyn:
Answer by Boreal(15235)   (Show Source):
You can put this solution on YOUR website! Nice job. It is quite easy to make a sign error in doing this. I made several. Your approach is just fine.
I set (3/4)m +3/4-(m^3/4)-(1/4)=0.25 for the 25th percentile.
The first term is straightforward; the second is subtracting a -3/4, so is a +3/4
the fourth term is (-1)^3 which is -1, then subtracted (+1) because the lower integral, then - again, 3 changes of sign.
Multiplying through by 4 and you get -m^3-1+3m+3=1
m^3-3m-1=0
m(q1)=-0.347
Md m=0
m(q3)=0.347
Answer by ikleyn(52776)  (Show Source):
You can put this solution on YOUR website! .
The pdf function is f(x) = 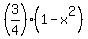 on the interval [-1,1].
The cdf function is antiderivative F(x) of f(x) such that F(-1) = 0.
So, the antiderivative is F(x) =  =  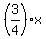-  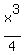+  , (1)
where C is the constant such that F(-1) = 0.
From this condition, you have this equation, substituting x= -1 into the formula (1)
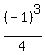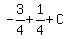 -  + = 0, or
 = 0, or
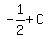 = 0,
which gives
C =  .
So, your antiderivative, or cdf function is
F(x) = - + .
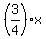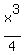Thus I complete calculating the needed cdf function.
Now my short COMMENT regarding your solution.
Your solution was INCORRECT.
You incorrectly found the cdf function,
because in integrating process you forgot about the constant term "C"
and forgot to satisfy the condition F(-1) = 0 for your cdf function.
I stop at this point leaving to complete the part 2 of the problem to you.
|
|
|
