Question 1168608: A data set includes 109 body temperatures of healthy adult humans having a mean of 98.3 F and a standard deviation of 0.54 F. Construct a 99% confidence interval estimate of the mean body temperature of all healthy humans. What does the sample suggest about the use of 98.6F as the mean body temperature?
Need to find
f < u< f
Answer by Theo(13342)   (Show Source): (Show Source):
You can put this solution on YOUR website! sample size is 109.
sample mean is 98.3
sample standard deviation is .54
population mean is assumed to be 98.6.
since you are dealing with the mean of a sample of a certain size, the standard error needs to be used rather than the standard deviation.
the formula for standard error is:
standard error = standard deviation / sqrt(sample size) = .54/sqrt(109) = .051723 rounded to 6 decimal places.
since you are dealing with a standard deviation extracted from the sample rather than from the population, the use of the t-score is indicated, rather than the z-score.
the z-score and the t-score are calculated the same way, except that the z-score gets the standard deviation from the population while the t-score gets the standard deviation from the sample.
the main difference between the z-score and the t-score, other than where the standard deviation is obtained, is in the calculation of probabilities of that score being inside or outside the confidence interval.
sample size is also a consideration.
with the z-score, the probabilities are the same, regardless of the sample size.
with the t-score, the probabilities are different, depending on the sample size.
here's a reference on when to use one or the other.
https://www.statisticshowto.com/probability-and-statistics/hypothesis-testing/t-score-vs-z-score/#:~:text=You%20must%20know%20the%20standard,%2C%20use%20the%20t%2Dscore.
the z-score / t-score formula is equal to (x - m) / s
the formula becomes z = (x - m) / s or t = (x - m) / s.
x is the raw score
m is the assumed mean
s is the standard error.
at 99% confidence level, the critical z-score will be plus or minus 2.58 rounded to 2 decimal places.
at 99% confidence level with 108 degrees of freedom, the critical t-score will be plus or minus 2.62 rounded to 2 decimal places.
they're not all that different because the sample size is large.
with a smaller sample size, you would see a bigger difference.
for example, if the sample size was 10, the critical z-score would be the same, but the critical t-score would be plus or minus 3.17.
regardless, the calculated z-score / t-score is -5.8.
this is well beyond the critical t-score or z-score, so the conclusion is that the mean body temperature of the population is probably closer to 98.3 than it is to 98.6.
a z-score calculator you can use is https://stattrek.com/online-calculator/normal.aspx
a t-score calculator you can use is https://stattrek.com/online-calculator/t-distribution.aspx
here are displays of the results from using these online calculators.
the first is the critical z-score calculation.
the second is the critical t-score calculation with 108 degrees of freedom.
the third is the critical t-score calculation with 10 degrees of freedom.
degrees of freedom are usually calculated as sample size minus 1.
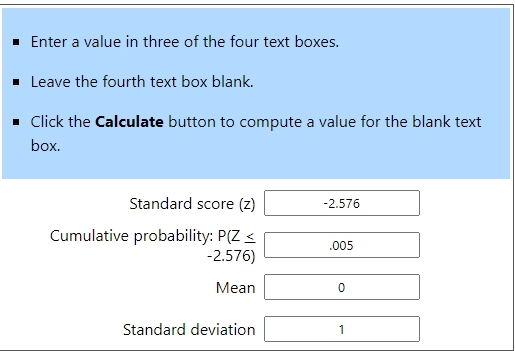
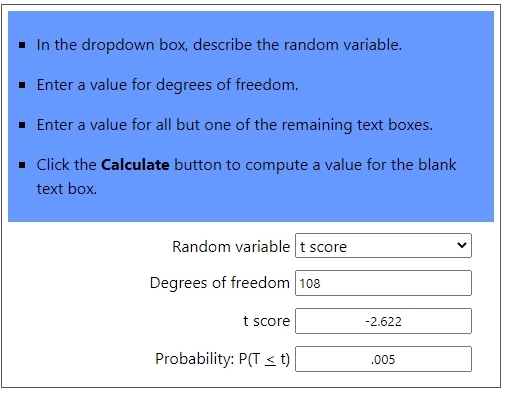
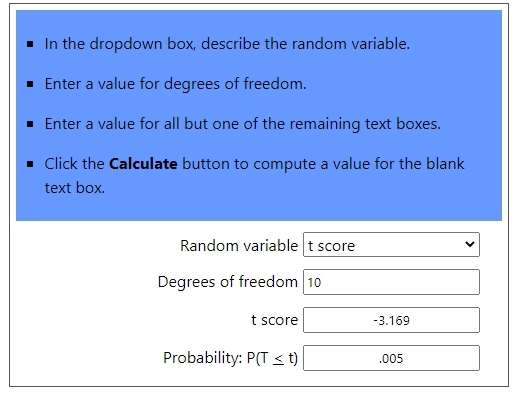
the confidence level is .99.
this means that .99 of the area under the normal distribution tables will be between the critical z-score / t-score.
since we are dealing with a two tail distribution, then .005 of the area will be to the left of the confidence interval and .005 of the area will be to the right of the confidence interval.
since the z-score / t-score calculation was negative, then we are looking for the critical z-score / t-score at the low end of the confidence interval for comparison purposes.
|
|
|