Question 1168486: Factories A, B and C produce computers. Factory A produces 3 times as many computers as factory C, and factory B produces 5 times as many computers as factory C. The probability that a computer produced by factory A is defective is 0.033, the probability that a computer produced by factory B is defective is 0.03, and the probability that a computer produced by factory C is defective is 0.035.
A computer is selected at random and it is found to be defective. What is the probability it came from factory A?
Answer by ikleyn(52932)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Factories A, B and C produce computers. Factory A produces 3 times as many computers as factory C,
and factory B produces 5 times as many computers as factory C. The probability that a computer produced by factory A
is defective is 0.033, the probability that a computer produced by factory B is defective is 0.03,
and the probability that a computer produced by factory C is defective is 0.035.
A computer is selected at random and it is found to be defective. What is the probability it came from factory A?
~~~~~~~~~~~~~
Let x = # of computers produced by factory C.
Then factory A produces 3x computers, while factory B produces 5x computers.
In total, the amount of all produced computers is Total = x + 3x + 5x = 9x.
The amount of defective computers produced by A is 0.033(3x); by factory B is 0.03*(5x), and by factory C is 0.035x.
The total amount of defective computers produced by A, B and C together is Total_defective = 0.033*(3x) + 0.03(5x) + 0.035x.
The problem's question is about the CONDITIONAL probability P(comp is from A | comp is defective).
By the definition of the conditional probability,
P(comp is from A | comp is defective) =  . (!)
The probability that the computer if from A and is defective is . (!)
The probability that the computer if from A and is defective is 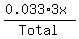 = = 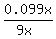 = 0.011.
The probability that the computer is defective is = 0.011.
The probability that the computer is defective is
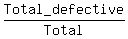 = = 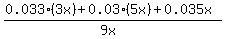 = = 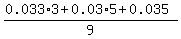 = 0.031556.
THEREFORE, the conditional probability (1) under the problem's question is
P(comp is from A | comp is defective) = = 0.031556.
THEREFORE, the conditional probability (1) under the problem's question is
P(comp is from A | comp is defective) =  = = 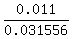 = 0.348587. ANSWER = 0.348587. ANSWER
Solved.
--------------
I presented the solution for you in the most detailed way.
When a person gains some experience, he (or she) can do such calculations in a couple of lines.
|
|
|