Question 1167448: Hello! I was having some difficulty on this question. I know there is 40 in the solution because there are 40 answers in total. However, I am not sure where to go from there. Any help is greatly appreciated! Thank you
Suppose that there are 10 questions in a multiple-choice exam with each question consisting of 4 choices. A student taking the exam forgot to study and decided to randomly guess on every question.
Find the probability that a student gets all the questions incorrect.
Find the probability that a student gets at least one correct.
Found 2 solutions by Boreal, ikleyn:
Answer by Boreal(15235)   (Show Source): (Show Source):
You can put this solution on YOUR website! all incorrect would be 0.75^40, since that the probability of getting a question wrong, assuming independence.
That is 0.000010
The complement, or 0.99999, is the probability of getting at least 1 right.
Answer by ikleyn(52794)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
1. Your thinking is INCORRECT.
2. Tutor @Boreal misread the problem and gave incorrect solution, too.
3. I came to bring a correct solution. See below.
Solution
For each of 10 questions, the probability to get incorrect answer is  = 0.75.
The probability to get all 10 answers incorrectly is, THEREFORE, = 0.75.
The probability to get all 10 answers incorrectly is, THEREFORE, 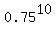 = 0.056314 = 5.6314%.
It is the answer to the first question.
The probability to get at least one correct answer is the COMPLEMENT to it, i.e. 1 - 0.056314 = 0.943686 = 94.3686%.
It is the answer to the second question. = 0.056314 = 5.6314%.
It is the answer to the first question.
The probability to get at least one correct answer is the COMPLEMENT to it, i.e. 1 - 0.056314 = 0.943686 = 94.3686%.
It is the answer to the second question.
Solved.
|
|
|