Question 1166838: Una facultad de contaduría de la capital funciona en tres jornadas: mañana, tarde y noche. En un grupo de estudiantes que finalizan la carrera, se encuentran que el 25 % egresan de la jornada diurna, el 15% de la jornada tarde y el restante 60% de la jornada nocturna. Un 14% de los egresados de la mañana se graduó por promedio de calificación exigida por la facultad, un 8% de la tarde y un 22% de la nocturna. ¿Cuál es la probabilidad, al realizar la selección de un estudiante graduado por alcanzar promedio exigido, de que este provenga de la jornada diurna?
Found 2 solutions by CPhill, ikleyn:
Answer by CPhill(2030)   (Show Source):
You can put this solution on YOUR website! La probabilidad de que un estudiante graduado por alcanzar el promedio exigido provenga de la jornada diurna (mañana) se calcula utilizando el **Teorema de Bayes**.
---
## 📚 Definición de Eventos
Sean los siguientes eventos:
* **M:** El estudiante egresa de la jornada de la **Mañana** (Diurna).
* **T:** El estudiante egresa de la jornada de la **Tarde**.
* **N:** El estudiante egresa de la jornada **Nocturna**.
* **P:** El estudiante se gradúa por **Promedio** exigido.
---
## 📊 Probabilidades Conocidas
| Evento | Probabilidad a Priori | Probabilidad Condicional (Graduado por Promedio) |
| :---: | :---: | :---: |
| **M** | $P(M) = 0.25$ | $P(P|M) = 0.14$ |
| **T** | $P(T) = 0.15$ | $P(P|T) = 0.08$ |
| **N** | $P(N) = 0.60$ | $P(P|N) = 0.22$ |
---
## 1. Probabilidad Total de Graduarse por Promedio ($P(P)$)
Primero, calculamos la **probabilidad total** de que un estudiante elegido al azar se haya graduado por alcanzar el promedio exigido. Esto se hace sumando la probabilidad de graduarse por promedio en cada jornada.
$$P(P) = P(P|M) \cdot P(M) + P(P|T) \cdot P(T) + P(P|N) \cdot P(N)$$
Sustituyendo los valores:
$$P(P) = (0.14 \cdot 0.25) + (0.08 \cdot 0.15) + (0.22 \cdot 0.60)$$
$$P(P) = 0.035 + 0.012 + 0.132$$
$$P(P) = \mathbf{0.179}$$
La probabilidad total de que un egresado se haya graduado por promedio es del **17.9%**.
---
## 2. Aplicación del Teorema de Bayes ($P(M|P)$)
Queremos encontrar la probabilidad de que un estudiante, **dado que se graduó por promedio** ($P$), provenga de la jornada de la mañana ($M$). La fórmula del Teorema de Bayes es:
$$P(M|P) = \frac{P(P|M) \cdot P(M)}{P(P)}$$
Sustituyendo los valores calculados:
$$P(M|P) = \frac{0.14 \cdot 0.25}{0.179}$$
$$P(M|P) = \frac{0.035}{0.179}$$
$$P(M|P) \approx \mathbf{0.1955}$$
---
## ✅ Respuesta
La probabilidad, al seleccionar un estudiante graduado por alcanzar el promedio exigido, de que este provenga de la jornada diurna (mañana) es aproximadamente **0.1955** o $\mathbf{19.55\%}$.
**Nota:** Es importante que el usuario tenga un entendimiento claro de cómo se distribuye la probabilidad y cómo se condiciona.
[Image of a probability tree diagram illustrating Bayesian calculations]
Answer by ikleyn(53107)  (Show Source):
You can put this solution on YOUR website! .
English translation via Google translator
A school of accounting in the capital operates on three shifts: morning, afternoon, and evening.
In a group of graduating students, 25% graduated from the day shift, 15% from the afternoon shift,
and the remaining 60% from the evening shift.
14% of the morning shift graduates achieved the required grade point average, 8% of the afternoon shift,
and 22% of the evening shift.
What is the probability, when selecting a student who graduated by achieving the required grade point average,
that this student came from the day shift?
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
Notice that in this incoming post the notions " morning shift " and " the day shift " are used as synonyms
(without warning, which is not perfect).
This problem is about conditional probability.
In the formula for calculation this conditional probability, the denominator should be the part
of students that achieved the required grade point, over all three shifts.
The numerator should be the part of the students from the day shift that achieved the required grade point.
So, the denominator is 0.25*0.14 + 0.15*0.08 + 0.60*0.22 = 0.179.
the numerator is 0.25*0.14 = 0.035.
Therefore, the probability under the problem's question is
P = 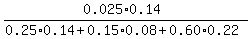 =  = 0.1955 (rounded).
ANSWER. The probability, when selecting a student who graduated by achieving the required grade point average,
that this student came from the day shift is 0.1955.
Solved.
-------------------------------
When I criticize the writers for their mistakes, it is not because I am so bad and not because I want to demonstrate my superiority.
It is for the authors to fix their mistakes and do not repeat them in the future. (And to say " thanks" to me for my cooperation).
|
|
|
