SOLUTION: Is it D? I want to check my answer. A teacher asked students in his class if they had any brothers or sisters. The results are shown below. What is the chance of randomly select

The diagram under the link shows, that there are 12 students in the class who have sister/sisters.


We can consider these 12 students as the population's part described by this fragment of the condition


           +------------------------------------+
           |  "given that they have a sister".  |
           +------------------------------------+


Of these 12 students, 5 have a brother/brothers.


Therefore, the probability under the problem's question is  .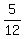


The  ANSWER  is option A.

    The important part is that the brothers or sisters can be not at / (or from) the given class.

    They (the sisters and the brothers) can be from totally different sets outside the class.



    Also, it is important to understand that the circles "brothers" and "sisters" on Venn  diagram DO NOT REPRESENT the girls or the boys.

    They represent partial populations of the class united according to the principle "has or not has this feature".


    It is similar to as if the students in the class were wearing special badges "have a brother", or "have a sister", OR BOTH (!)