Question 1159882: 7 men and 3 women are ranked according to their scores on an exam. Assume that no two scores are alike, and that all 10! possible rankings are equally likely. Let X denote the highest ranking achieved by a man (so X=1 indicates that a man achieved the highest score on the exam). Find each of the following:
P(X=1)=
P(X=2)=
P(X=3)=
P(X=7)=
Answer by ikleyn(52781)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
7 men and 3 women are ranked according to their scores on an exam. Assume that no two scores are alike,
and that all 10! possible rankings are equally likely. Let X denote the highest ranking achieved by a man
(so X=1 indicates that a man achieved the highest score on the exam). Find each of the following:
(a) P(X=1) =
(b) P(X=2) =
(c) P(X=3) =
(d) P(X=7) =
~~~~~~~~~~~~~~~~~~~~~~~~~~
(a) X=1 means that one of the 7 men is in the first position,
while the rest 6 men and 3 women are distributed in positions from 2 to 10 in arbitrary ways.
The number of such possible outcomes is 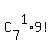 = 7*9!,
and to find the probability P(X=1), we should relate 7*9! to 10!.
It gives P(X=1) = = 7*9!,
and to find the probability P(X=1), we should relate 7*9! to 10!.
It gives P(X=1) = 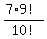 = = 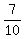 = 0.7.
It is the ANSWER to (a).
(b) X=2 means that one of the 3 women is in the first position and one of the 7 men is in the second position,
while the rest 3-1 = 2 women and 7-1 = 6 men are distributed in positions from 3 to 10 in arbitrary ways.
The number of such possible outcomes is = 0.7.
It is the ANSWER to (a).
(b) X=2 means that one of the 3 women is in the first position and one of the 7 men is in the second position,
while the rest 3-1 = 2 women and 7-1 = 6 men are distributed in positions from 3 to 10 in arbitrary ways.
The number of such possible outcomes is  = 3*7*8!,
and to find the probability P(X=2), we should relate 3*7*8! to 10!.
It gives P(X=2) = = 3*7*8!,
and to find the probability P(X=2), we should relate 3*7*8! to 10!.
It gives P(X=2) = 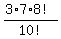 = =  = = 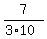 = = 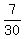 .
It is the ANSWER to (b).
(c) X=3 means that two of the 3 women are in the first and in the second positions and one of the 7 men
is in the third position,
while the rest 3-2 = 1 women and 7-1 = 6 men are distributed in positions from 3 to 10 in arbitrary ways.
The number of such possible outcomes is .
It is the ANSWER to (b).
(c) X=3 means that two of the 3 women are in the first and in the second positions and one of the 7 men
is in the third position,
while the rest 3-2 = 1 women and 7-1 = 6 men are distributed in positions from 3 to 10 in arbitrary ways.
The number of such possible outcomes is 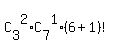 = = 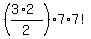 = 3*7*7!,
and to find the probability P(X=3), we should relate 3*7*7! to 10!.
It gives P(X=3) = = 3*7*7!,
and to find the probability P(X=3), we should relate 3*7*7! to 10!.
It gives P(X=3) = 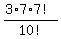 = =  = = 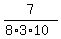 = = 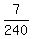 .
It is the ANSWER to (c).
(d) X=7 means that some man is in the 7th positions and there no men in positions from 1 to 6.
But this configuration is not possible (which is obvious), so
P(X=7) = 0.
It is the ANSWER to (d). .
It is the ANSWER to (c).
(d) X=7 means that some man is in the 7th positions and there no men in positions from 1 to 6.
But this configuration is not possible (which is obvious), so
P(X=7) = 0.
It is the ANSWER to (d).
Thus, all the questions are answered, and the problem is solved completely.
|
|
|