.
(1) 6 cars are picked randomly from a garage which has 4 blacks cars and 2 white cars and 4 red cars
find the probability of getting at MOST 1 red car.
(2) 6 cars are picked randomly from a garage which has 4 black cars and 2 white cars and 4 red cars
find the probability of getting at LEAST 1 red car
~~~~~~~~~~~~~~~~~~~~~~~
(1) Find the probability of getting at MOST 1 red car
The total number of cars in the garage is 4 + 2 + 4 = 10.
The probability under the question is the sum of probabilities to get 0 red cars or to get 1 red car,
P = P(0) + P(1).
The number of ways to get 0 red cars is 1: it is the case to get 4 black and 2 white cars.
The number of ways to get 1 red car of 6 picked cars is equal to the number to comprise 5 cars from (4+2) = 6 cars
of the not-red color, multiplied by 4, which is the number to select 1 red car from 4 red cars.
So, the number of ways to get 1 red car of 6 picked cars is
C(6,5)*(C4,1) = 6*4 = 24.
The total number to get 6 cars from 10 cars is C(10,6) = 210.
Therefore, the probability under the question (1) is 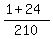 =
=  =
= 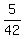 . ANSWER
. ANSWER
Part (1) is solved.
(2) Find the probability of getting at LEAST 1 red car
The probability of getting at LEAST 1 red car is the COMPLEMENT to the probability to get no one red car.
There is only one way to get no one red car: it is to get 4 black cars and 2 white cars
So, the probability to get no one red car is P' = 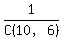 =
= 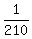 .
Thus, the answer to question (2) is P = 1 - P' = 1 -
.
Thus, the answer to question (2) is P = 1 - P' = 1 - 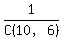 = 1 -
= 1 - 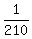 =
= 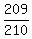 .
.
Part (2) is solved, too.