You can
put this solution on YOUR website! An organization consisting of 27 women and 11 men needs to select from its ranks
a committee of 7 people.
In how many possible ways can the committee be formed so that it contains
exactly two men?
7 people with exactly 2 men also have exactly 5 women.
Choose the 2 men any of "11 CHOOSE 2" or 11C2 = 55 ways
For each of those 55 ways to choose the 2 men, there are
"27 CHOOSE 5" or 80730 ways to choose the 5 women. That
amounts to (55)(80730) or 4440150 ways.
The number of ways to choose ANY 7 from the 27+11=38 people is
"38 CHOOSE 7" or 38C7 = 12620256 ways.
So the probability of choosing 7 with exactly 2 men is
4440150 ways out of 12620256 or
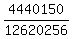which reduces to
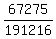and which is approximately 35.2% of the time 2 men and 2 women
will be chosen.
Edwin
