SOLUTION: There are 16 students giving final presentations in your history course. (a) Three students present per day. How many presentation orders are possible for the first day? (b)

(a)  "How many presentation orders are possible for the first day" = 16*15*14.


     Any of 16 students can give 1-st presentation.

     Any of remaining 15 students can give 2-nd presentation.

     Any of remaining 14 students can give 3-rd presentation.


     The total is the product of these factors.



(b)  The number of orders in this case is


         N = 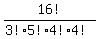 = 50450400.


     This formula is standard for such kind of problems on arranging the set containing groups of indistinguishable elements.


     The factorials in denominator serve to account multiplicities of indistinguishable elements in groups.




     Probably, it would be more clear, if I retell it in other way.


     We may think that each of 16 students simply carries the name of the unit "A", "B", "C" and "D",

     instead of making real presentation.


     Then the question is: how many 16-letter words do exist, written in  4-letter alphabet A, B, C and D, in a way that
      letter A occurs 4 times; letter B occurs 3 times; letter C occurs 5 times, and letter D occurs 4 times.


     Then the answer to this question is EXACTLY as I described it above.