Question 1153010: Starbucks has found that 25% of customers purchase more than one cup of coffee per day from their shops.Suppose you randomly choose 200 of today's Starbucks customers.Find the probability that no less than 34% of them purchased more than one cup of coffee from Starbucks.
Answer by jim_thompson5910(35256)   (Show Source): (Show Source):
You can put this solution on YOUR website!
Define a success to be the event a customer purchases more than one cup of coffee per day.
p = probability of success
p = 0.25
n = 200 is the sample size
The phrasing "no less than 34% of them [the 200 sampled]" means
34% of 200 = 0.34*200 = 68
So we can rephrase "no less than 34% of them" into "no less than 68" which is equivalent to saying "at least 68"
In other words, we want to find  where X = number of customers who purchase more than one cup of coffee. where X = number of customers who purchase more than one cup of coffee.
The value of X ranges from 0 to 200, and it is a whole number. If X = 0, then no people bought more than one cup of coffee. If X = 1, then exactly one person bought more than one cup. Etc etc.
Normally we would use a binomial distribution (since we have independent trials and each trial is a yes/no question), but computing  will be tedious through the binomial formula. will be tedious through the binomial formula.
Instead, it is better to a get normal approximation.
Note that,
n*p = 200*0.25 = 50
n*(1-p) = 200*(1-0.25) = 200*0.75 = 150
are both greater than 5. Since 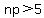 and and 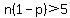 , we can use a normal approximation to the binomial. , we can use a normal approximation to the binomial.
Compute the mean (mu) and standard deviation (sigma)
mu = population mean
mu = n*p
mu = 200*0.25
mu = 50
sigma = sqrt(n*p*(1-p))
sigma = sqrt(200*0.25*(1-0.25))
sigma = 6.12372435695794
Instead of finding  , we need to find , we need to find 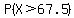 . This is due to the Continuity Correction Factor as shown on this page . This is due to the Continuity Correction Factor as shown on this page
https://www.statisticshowto.datasciencecentral.com/probability-and-statistics/binomial-theorem/normal-approximation-to-the-binomial/
(see part 2 of that page)
Compute the z score to the raw score of x = 67.5
z = (x - mu)/sigma
z = (67.5 - 50)/6.12372435695794
z = 2.85773803324704
z = 2.86
This means  \approx P(Z > 2.86))
Use a table such as this one
http://www.z-table.com/
(a similar one can be found in the back of your stat textbook)
to find that
P(Z < 2.86) = 0.9979
So,
P(Z > 2.86) = 1-P(Z < 2.86)
P(Z > 2.86) = 1-0.9979
P(Z > 2.86) = 0.0021
Answer: 0.0021
|
|
|