Question 1152183: a two digit number has each of the digits {0, 1, 2, 3, 4, 5, 6} appearing exactly once. what is the probability that the number is divisible by two?
Answer by math_helper(2461)   (Show Source): (Show Source):
You can put this solution on YOUR website!
Assuming 01, 02, etc. are considered two digit numbers:
P(even number formed from random selection of two digits, without replacement) = P(even number chosen for ten's digit AND even number chosen for one's digit) +
P(odd number chosend for ten's digit AND even number chosen for one's digit)
= (4/7)(3/6) + (3/7)(4/6)
= 12/42 + 12/42
= 24/42
= 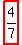
This matches the proportion of even digits in the set to the total number of digits in the set. Coincidence?
-----
Expanding the problem to 3 digit numbers you will find P(even) = 4/7
Expanding to 4 digit numbers also gives P(even) = 4/7
-----
The above cases assume 0 as a leading digit counts, if 0 is disallowed as a leading digit then for two-digit cases P(even) = (3/7)(3/6)+(3/7)(4/6) = 1/2.
|
|
|